KendallRankCorrelation[xlist,ylist]
gives Kendall's rank correlation coefficient ![]() for the real-valued vectors xlist and ylist.
for the real-valued vectors xlist and ylist.


KendallRankCorrelation
KendallRankCorrelation[xlist,ylist]
gives Kendall's rank correlation coefficient ![]() for the real-valued vectors xlist and ylist.
for the real-valued vectors xlist and ylist.
更多信息和选项
- To use KendallRankCorrelation, you first need to load the Multivariate Statistics Package using Needs["MultivariateStatistics`"].
- Kendall's rank correlation coefficient is a measure of association based on the relative order of consecutive elements in the two lists.
- Kendall's rank correlation coefficient between
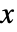 and
and 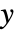 is given by
is given by 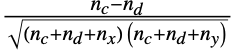 , where
, where 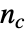 is the number of concordant pairs of observations,
is the number of concordant pairs of observations, 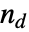 is the number of discordant pairs,
is the number of discordant pairs, 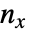 is the number of ties involving only the
is the number of ties involving only the 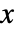 variable, and
variable, and 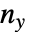 is the number of ties involving only the
is the number of ties involving only the 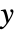 variable.
variable. - A concordant pair of observations
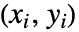 and
and 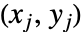 is one such that both
is one such that both 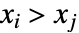 and
and 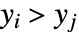 or both
or both 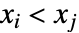 and
and 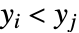 . A discordant pair of observations is one such that
. A discordant pair of observations is one such that 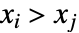 and
and 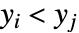 or
or 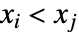 and
and 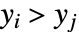 .
. - The arguments xlist and ylist can be any real‐valued vectors of equal length.
文本
Wolfram Research (2007),KendallRankCorrelation,Wolfram 语言函数,https://reference.wolfram.com/language/MultivariateStatistics/ref/KendallRankCorrelation.html.
CMS
Wolfram 语言. 2007. "KendallRankCorrelation." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/MultivariateStatistics/ref/KendallRankCorrelation.html.
APA
Wolfram 语言. (2007). KendallRankCorrelation. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/MultivariateStatistics/ref/KendallRankCorrelation.html 年
BibTeX
@misc{reference.wolfram_2025_kendallrankcorrelation, author="Wolfram Research", title="{KendallRankCorrelation}", year="2007", howpublished="\url{https://reference.wolfram.com/language/MultivariateStatistics/ref/KendallRankCorrelation.html}", note=[Accessed: 05-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_kendallrankcorrelation, organization={Wolfram Research}, title={KendallRankCorrelation}, year={2007}, url={https://reference.wolfram.com/language/MultivariateStatistics/ref/KendallRankCorrelation.html}, note=[Accessed: 05-December-2025]}