MultivariateStatistics`
MultivariateStatistics`

SpearmanRankCorrelation

As of Version 9.0, SpearmanRankCorrelation has been renamed to SpearmanRho and is part of the built-in Wolfram Language kernel.

SpearmanRankCorrelation[xlist,ylist]

gives Spearman's rank correlation coefficient for the real‐valued vectors xlist and ylist.

Details and Options

  • To use SpearmanRankCorrelation, you first need to load the Multivariate Statistics Package using Needs["MultivariateStatistics`"].
  • Spearman's rank correlation coefficient is a measure of association based on the rank differences between two lists.
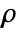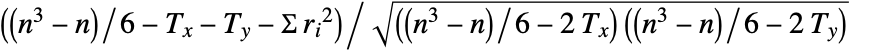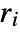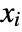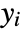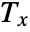  • Spearman's is given by , where n=Length[xlist], is the rank difference between and , is the correction term for ties in xlist, and 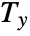is the correction term for ties in ylist.
  • The arguments xlist and ylist can be any real‐valued vectors of equal length.

Examples

Basic Examples  (1)

Spearman's rank correlation for two vectors:

Wolfram Research (2007), SpearmanRankCorrelation, Wolfram Language function, https://reference.wolfram.com/language/MultivariateStatistics/ref/SpearmanRankCorrelation.html.

Text

Wolfram Research (2007), SpearmanRankCorrelation, Wolfram Language function, https://reference.wolfram.com/language/MultivariateStatistics/ref/SpearmanRankCorrelation.html.

CMS

Wolfram Language. 2007. "SpearmanRankCorrelation." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/MultivariateStatistics/ref/SpearmanRankCorrelation.html.

APA

Wolfram Language. (2007). SpearmanRankCorrelation. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/MultivariateStatistics/ref/SpearmanRankCorrelation.html

BibTeX

@misc{reference.wolfram_2024_spearmanrankcorrelation, author="Wolfram Research", title="{SpearmanRankCorrelation}", year="2007", howpublished="\url{https://reference.wolfram.com/language/MultivariateStatistics/ref/SpearmanRankCorrelation.html}", note=[Accessed: 24-April-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_spearmanrankcorrelation, organization={Wolfram Research}, title={SpearmanRankCorrelation}, year={2007}, url={https://reference.wolfram.com/language/MultivariateStatistics/ref/SpearmanRankCorrelation.html}, note=[Accessed: 24-April-2024 ]}