WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

KendallTau
✖
KendallTau

✖
KendallTau[v1,v2]

gives Kendall's rank correlation coefficient for the vectors v1 and v2.

✖

gives Kendall's rank correlation coefficients for the matrix m.

✖
KendallTau[m1,m2]

gives Kendall's rank correlation coefficients for the matrices m1 and m2.

✖
KendallTau[dist]

gives Kendall's rank correlation matrix for the multivariate symbolic distribution dist.

✖
KendallTau[dist,i,j]

gives the ^(th) Kendall rank correlation for the multivariate symbolic distribution dist.

Details

  • KendallTau[v1,v2] gives Kendall's rank correlation coefficient between v1 and v2.
  • Kendall's is a measure of monotonic association based on the relative order of consecutive elements in the two lists.
  • Kendall's between and is given by , where is the number of concordant pairs of observations, is the number of discordant pairs, is the number of ties involving only the variable, and is the number of ties involving only the variable.
  • A concordant pair of observations and is one such that both and or both and . A discordant pair of observations is one such that and or and .
  • The tie-corrected version of Kendall's returned is sometimes referred to as Kendall's , or tau-b.
  • The arguments v1 and v2 can be any real‐valued vectors of equal length.
  • For a matrix m with columns, KendallTau[m] is a × matrix of the rank‐correlations between columns of m.
  • For an × matrix m1 and an × matrix m2, KendallTau[m1,m2] is a × matrix of the rank‐correlations between columns of m1 and columns of m2.
  • KendallTau[dist,i,j] is the probability of concordance minus the probability of discordance Probability[(x1-x2)(y1-y2)>0,{{x1,y1}disti,j,{x2,y2}disti,j}]-Probability[(x1-x2)(y1-y2)<0,{{x1,y1}disti,j,{x2,y2}disti,j}] where disti,j is the ^(th) marginal of dist.
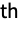  • KendallTau[dist] gives a matrix where the ^(th) entry is given by KendallTau[dist,i,j].

Examples

open allclose all

Basic Examples  (4)Summary of the most common use cases

Kendall's for two vectors:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-gugb6d
In[3]:=3
✖
https://wolfram.com/xid/0k8aytrlbs44d-fulot0
Out[3]=3

Kendall's for a matrix:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-9un6t
In[2]:=2
✖
https://wolfram.com/xid/0k8aytrlbs44d-hz9gv1

Kendall's for two matrices:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-bv14aj
In[2]:=2
✖
https://wolfram.com/xid/0k8aytrlbs44d-ce2wv
In[3]:=3
✖
https://wolfram.com/xid/0k8aytrlbs44d-i51zwj

Compute Kendall's for a bivariate distribution:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-f7dh9d
In[2]:=2
✖
https://wolfram.com/xid/0k8aytrlbs44d-mzz2lg

Compare to a simulated value:

In[3]:=3
✖
https://wolfram.com/xid/0k8aytrlbs44d-nwpxl1

Scope  (7)Survey of the scope of standard use cases

Data  (4)

Exact input yields exact output:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-eta06h
Out[1]=1

Approximate input yields approximate output:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-bxeync
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0k8aytrlbs44d-04fgr
Out[2]=2

Works with large arrays:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-kt50m4
Out[1]=1

SparseArray data can be used:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-gighjo

Distributions and Processes  (3)

Kendall's matrix for a continuous multivariate distribution:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-fnv00k
In[2]:=2
✖
https://wolfram.com/xid/0k8aytrlbs44d-tekwa
Out[2]=2

Kendall's matrix for derived distributions:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-c3a9y
In[2]:=2
✖
https://wolfram.com/xid/0k8aytrlbs44d-cy97of
In[3]:=3
✖
https://wolfram.com/xid/0k8aytrlbs44d-etkwz

Data distribution:

In[4]:=4
✖
https://wolfram.com/xid/0k8aytrlbs44d-hxjash
In[5]:=5
✖
https://wolfram.com/xid/0k8aytrlbs44d-gm1a47
In[6]:=6
✖
https://wolfram.com/xid/0k8aytrlbs44d-edj4ah

Kendall's matrix for a random process at times and :

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-hv1ygl

Applications  (4)Sample problems that can be solved with this function

Kendall's is typically used to detect linear dependence between two vectors:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-fhbudj

The absolute magnitude of tends to 1 given strong linear dependence:

In[3]:=3
✖
https://wolfram.com/xid/0k8aytrlbs44d-rv8j1
Out[3]=3

The value tends to 0 for linearly independent vectors:

In[4]:=4
✖
https://wolfram.com/xid/0k8aytrlbs44d-bo8mij
Out[4]=4

Kendall's can be used to measure linear association:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-d9hc8
In[2]:=2
✖
https://wolfram.com/xid/0k8aytrlbs44d-bmf8jn
Out[2]=2

Kendall's can only detect monotonic association:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-7nvfr
In[2]:=2
✖
https://wolfram.com/xid/0k8aytrlbs44d-nazb6e
In[3]:=3
✖
https://wolfram.com/xid/0k8aytrlbs44d-j9qi3
In[4]:=4
✖
https://wolfram.com/xid/0k8aytrlbs44d-gtfa0z
Out[4]=4

HoeffdingD can be used to detect other dependence structures:

In[5]:=5
✖
https://wolfram.com/xid/0k8aytrlbs44d-jor85u
Out[5]=5

A series of factors was measured in 506 Boston suburbs with the intention of determining how these factors are related to home price. Significant correlations among factors such as nitrogen oxide concentration and median home price serve as a reminder that correlation does not imply causation:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-393icd
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0k8aytrlbs44d-m2ro2p
In[3]:=3
✖
https://wolfram.com/xid/0k8aytrlbs44d-eyz3fx

A scatter plot matrix comparing the percentage of non-retail businesses, nitrogen oxide concentration, and median home value:

In[4]:=4
✖
https://wolfram.com/xid/0k8aytrlbs44d-jmvxe
Out[4]=4

Kendall's matrix for the scatter plot matrix:

In[5]:=5
✖
https://wolfram.com/xid/0k8aytrlbs44d-bgan7z

KendallTauTest suggests home values drop with increasing nitrogen oxide concentrations:

In[6]:=6
✖
https://wolfram.com/xid/0k8aytrlbs44d-ei3usk
Out[6]=6

Properties & Relations  (8)Properties of the function, and connections to other functions

Kendall's ranges from -1 to 1 for high negative and high positive association, respectively:

In[4]:=4
✖
https://wolfram.com/xid/0k8aytrlbs44d-fvojjd
In[6]:=6
✖
https://wolfram.com/xid/0k8aytrlbs44d-cp90d4
Out[6]=6
In[7]:=7
✖
https://wolfram.com/xid/0k8aytrlbs44d-mp4oro
Out[7]=7

Kendall's matrix is symmetric:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-31bc2
In[2]:=2
✖
https://wolfram.com/xid/0k8aytrlbs44d-mmzf9d
Out[2]=2

The diagonal elements of Kendall's matrix are 1:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-o1vsb7
In[2]:=2
✖
https://wolfram.com/xid/0k8aytrlbs44d-h7qlge
Out[2]=2

Kendall's is related to SpearmanRho:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-hbkym

SpearmanRho tends to be about given weak linear association:

In[2]:=2
✖
https://wolfram.com/xid/0k8aytrlbs44d-mts4te
Out[2]=2

Use KendallTauTest to test for independence:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-l4v2w
In[2]:=2
✖
https://wolfram.com/xid/0k8aytrlbs44d-eetjj
Out[2]=2

Alternatively, use IndependenceTest to automatically select an appropriate test:

In[3]:=3
✖
https://wolfram.com/xid/0k8aytrlbs44d-kv172
Out[3]=3

Kendall's will attain 1 or -1 if the variables are perfectly monotonically related:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-xln2s
In[2]:=2
✖
https://wolfram.com/xid/0k8aytrlbs44d-dde2tx
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0k8aytrlbs44d-gm71p
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0k8aytrlbs44d-kylhyv
Out[4]=4

This is in contrast to Correlation, which strictly measures linear association:

In[5]:=5
✖
https://wolfram.com/xid/0k8aytrlbs44d-f40mz2
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0k8aytrlbs44d-m22vt
Out[6]=6

Kendall's for a continuous bivariate distribution:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-bfewud
In[2]:=2
✖
https://wolfram.com/xid/0k8aytrlbs44d-ewdode
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0k8aytrlbs44d-grblhu
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0k8aytrlbs44d-hqcqde
Out[4]=4

Kendall's for discrete distributions accounts for the distribution of ties:

In[1]:=1
✖
https://wolfram.com/xid/0k8aytrlbs44d-xeczx
In[2]:=2
✖
https://wolfram.com/xid/0k8aytrlbs44d-mewcqm
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0k8aytrlbs44d-ck6mtm
In[4]:=4
✖
https://wolfram.com/xid/0k8aytrlbs44d-frwxj
In[5]:=5
✖
https://wolfram.com/xid/0k8aytrlbs44d-68hk3
Out[5]=5

Compare to a simulated value with and without corrections for ties:

In[6]:=6
✖
https://wolfram.com/xid/0k8aytrlbs44d-ev6nh6
In[7]:=7
✖
https://wolfram.com/xid/0k8aytrlbs44d-016xf
Out[7]=7

Tie-corrected expectation:

In[8]:=8
✖
https://wolfram.com/xid/0k8aytrlbs44d-e15ep0
Out[8]=8

No correction for ties:

In[9]:=9
✖
https://wolfram.com/xid/0k8aytrlbs44d-cm4yha
Out[9]=9
Wolfram Research (2012), KendallTau, Wolfram Language function, https://reference.wolfram.com/language/ref/KendallTau.html.
✖
Wolfram Research (2012), KendallTau, Wolfram Language function, https://reference.wolfram.com/language/ref/KendallTau.html.

Text

Wolfram Research (2012), KendallTau, Wolfram Language function, https://reference.wolfram.com/language/ref/KendallTau.html.

✖
Wolfram Research (2012), KendallTau, Wolfram Language function, https://reference.wolfram.com/language/ref/KendallTau.html.

CMS

Wolfram Language. 2012. "KendallTau." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/KendallTau.html.

✖
Wolfram Language. 2012. "KendallTau." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/KendallTau.html.

APA

Wolfram Language. (2012). KendallTau. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KendallTau.html

✖
Wolfram Language. (2012). KendallTau. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KendallTau.html

BibTeX

@misc{reference.wolfram_2025_kendalltau, author="Wolfram Research", title="{KendallTau}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/KendallTau.html}", note=[Accessed: 04-April-2025 ]}

✖
@misc{reference.wolfram_2025_kendalltau, author="Wolfram Research", title="{KendallTau}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/KendallTau.html}", note=[Accessed: 04-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_kendalltau, organization={Wolfram Research}, title={KendallTau}, year={2012}, url={https://reference.wolfram.com/language/ref/KendallTau.html}, note=[Accessed: 04-April-2025 ]}

✖
@online{reference.wolfram_2025_kendalltau, organization={Wolfram Research}, title={KendallTau}, year={2012}, url={https://reference.wolfram.com/language/ref/KendallTau.html}, note=[Accessed: 04-April-2025 ]}