KendallTauTest

KendallTauTest[v1,v2]

tests whether the vectors v1 and v2 are independent.

KendallTauTest[m1,m2]

tests whether the matrices m1 and m2 are independent.

KendallTauTest[…,"property"]

returns the value of "property".

Details and Options

  • KendallTauTest performs a hypothesis test on v1 and v2 with null hypothesis 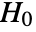that the vectors are independent, and alternative hypothesis 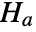that they are not.
  • By default, a probability value or 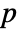-value is returned.
  • A small 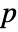-value suggests that it is unlikely that 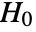is true.
  • The arguments v1 and v2 can be any real-valued vectors or matrices of equal length.
  • KendallTauTest is based on Kendall's rank correlation 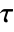computed by KendallTau[v1,v2].
  • For testing matrices, the test statistic is based on the ratio inner standardized spatial signs and ranks and asymptotically follows a ChiSquareDistribution[r*s] where r and s are the dimension of m1 and m2, respectively.
  • KendallTauTest[v1,v2,"HypothesisTestData"] returns a HypothesisTestData object htd that can be used to extract additional test results and properties using the form htd["property"].
  • KendallTauTest[v1,v2,"property"] can be used to directly give the value of "property".
  • Properties related to the reporting of test results include:
  • "DegreesOfFreedom"the degrees of freedom used in the test
    "PValue"the 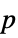-value of the test
    "PValueTable"formatted table containing the 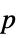-value
    "ShortTestConclusion"a short description of the conclusion of the test
    "TestConclusion"a description of the conclusion of the test
    "TestData"a list containing the test statistic and 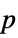-value
    "TestDataTable"formatted table of the 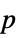-value and test statistic
    "TestStatistic"the test statistic
    "TestStatisticTable"formatted table containing the test statistic
  • The following options can be used:
  • AlternativeHypothesis "Unequal"the inequality for the alternative hypothesis
    MaxIterations Automaticmax iterations for multivariate test
    Method Automaticthe method to use for computing 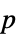-values
    SignificanceLevel 0.05cutoff for diagnostics and reporting
  • For tests of independence, a cutoff 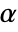is chosen such that 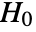is rejected only if 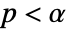. The value of 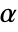used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. By default, 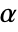is set to 0.05.

Examples

open allclose all

Basic Examples  (2)

Test whether two vectors are independent:

Test whether two matrices are independent:

At the 0.05 level, there is insufficient evidence to reject independence:

Scope  (8)

Testing  (5)

Test whether two vectors are independent:

The -values are typically large when the vectors are independent:

The -values are typically small when there are dependencies:

Test whether two matrices are independent:

The -values are typically small for dependent matrices:

The -values are typically large when matrices are independent:

Create a HypothesisTestData object for repeated property extraction:

The properties available for extraction:

Extract some properties from the HypothesisTestData object:

The -value and test statistic from the test:

Extract any number of properties simultaneously:

The -value and test statistic from the test:

Reporting  (3)

Tabulate the results from the test:

A table of the test results:

Retrieve the entries from a test table for customized reporting:

Tabulate the -value or test statistic:

The -value from the table:

The test statistic from the table:

Options  (9)

AlternativeHypothesis  (3)

A two-sided test is performed by default:

Perform a two-sided test or a one-sided alternative:

A two-sided test:

The two one-sided alternatives:

The multivariate test is inherently two-sided:

This is due to the shape of the null distribution:

MaxIterations  (1)

Set the maximum number of iterations to use for multivariate test:

By default, is used:

Lowering the setting can shorten compute times but may result in failed convergence:

Method  (4)

By default, -values are computed using asymptotic test statistic distributions:

The -value can be obtained using permutation methods:

Set the number of permutations to use:

By default, random permutations are used:

Set the seed used for generating random permutations:

SignificanceLevel  (1)

The significance level is used for "TestConclusion" and "ShortTestConclusion":

Properties & Relations  (5)

For vector to vector comparisons, the test statistic is computed as KendallTau:

In matrix comparisons, the test statistic follows a ChiSquareDistribution[r*s]:

For matrix comparisons, the test statistic is invariant under affine transformations:

IndependenceTest can be used to select an appropriate test of independence:

KendallTauTest is one of the available tests:

KendallTauTest only detects monotonic dependence:

HoeffdingDTest can be used to detect a wider variety of dependence structures:

Neat Examples  (1)

Compute the statistic when the null hypothesis is true:

The test statistic given a particular alternative:

Compare the distributions of the test statistics:

Wolfram Research (2012), KendallTauTest, Wolfram Language function, https://reference.wolfram.com/language/ref/KendallTauTest.html.

Text

Wolfram Research (2012), KendallTauTest, Wolfram Language function, https://reference.wolfram.com/language/ref/KendallTauTest.html.

CMS

Wolfram Language. 2012. "KendallTauTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/KendallTauTest.html.

APA

Wolfram Language. (2012). KendallTauTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KendallTauTest.html

BibTeX

@misc{reference.wolfram_2024_kendalltautest, author="Wolfram Research", title="{KendallTauTest}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/KendallTauTest.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_kendalltautest, organization={Wolfram Research}, title={KendallTauTest}, year={2012}, url={https://reference.wolfram.com/language/ref/KendallTauTest.html}, note=[Accessed: 21-November-2024 ]}