SpearmanRankTest[v1,v2]
tests whether the vectors v1 and v2 are independent.
SpearmanRankTest[m1,m2]
tests whether the matrices m1 and m2 are independent.
SpearmanRankTest[…,"property"]
returns the value of "property".


SpearmanRankTest
SpearmanRankTest[v1,v2]
tests whether the vectors v1 and v2 are independent.
SpearmanRankTest[m1,m2]
tests whether the matrices m1 and m2 are independent.
SpearmanRankTest[…,"property"]
returns the value of "property".
Details and Options


- SpearmanRankTest performs a hypothesis test on v1 and v2 with null hypothesis
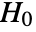 that the vectors are independent, and alternative hypothesis
that the vectors are independent, and alternative hypothesis 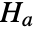 that they are not.
that they are not. - By default a probability value or
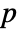 -value is returned.
-value is returned. - A small
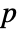 -value suggests that it is unlikely that
-value suggests that it is unlikely that 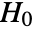 is true.
is true. - The arguments v1 and v2 can be any real-valued vectors or matrices of equal length.
- SpearmanRankTest is based on Spearman's rank correlation
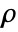 computed by SpearmanRho[v1,v2].
computed by SpearmanRho[v1,v2]. - For testing matrices the test statistic is based on inner standardized spatial ranks and asymptotically follows a ChiSquareDistribution[r*s] where r and s are the dimension of m1 and m2, respectively. The test is invariant under affine transformations.
- SpearmanRankTest[v1,v2,"HypothesisTestData"] returns a HypothesisTestData object htd that can be used to extract additional test results and properties using the form htd["property"].
- SpearmanRankTest[v1,v2,"property"] can be used to directly give the value of "property".
- Properties related to the reporting of test results include:
-
"DegreesOfFreedom" the degrees of freedom used in the test "PValue" the 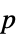 -value of the test
-value of the test"PValueTable" formatted table containing the 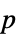 -value
-value"ShortTestConclusion" a short description of the conclusion of the test "TestConclusion" a description of the conclusion of the test "TestData" a list containing the test statistic and 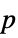 -value
-value"TestDataTable" formatted table of the 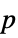 -value and test statistic
-value and test statistic"TestStatistic" the test statistic "TestStatisticTable" formatted table containing the test statistic - The following options can be used:
-
AlternativeHypothesis "Unequal" the inequality for the alternative hypothesis MaxIterations Automatic max iterations for multivariate test Method Automatic the method to use for computing 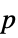 -values
-valuesSignificanceLevel 0.05 cutoff for diagnostics and reporting - For tests of independence, a cutoff
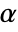 is chosen such that
is chosen such that 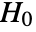 is rejected only if
is rejected only if 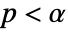 . The value of
. The value of 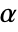 used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. By default
used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. By default 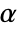 is set to 0.05.
is set to 0.05.
Examples
open all close allBasic Examples (2)
Scope (8)
Testing (5)
Test whether two vectors are independent:
The ![]() -values are typically large when the vectors are independent:
-values are typically large when the vectors are independent:
The ![]() -values are typically small when there are dependencies:
-values are typically small when there are dependencies:
Test whether two matrices are independent:
The ![]() -values are typically small for dependent matrices:
-values are typically small for dependent matrices:
The ![]() -values are typically large when matrices are independent:
-values are typically large when matrices are independent:
Create a HypothesisTestData object for repeated property extraction:
The properties available for extraction:
Extract some properties from the HypothesisTestData object:
The ![]() -value and test statistic from the test:
-value and test statistic from the test:
Options (9)
AlternativeHypothesis (3)
MaxIterations (1)
Method (4)
Properties & Relations (9)
For vector-to-vector comparisons the test statistic is computed as SpearmanRho:
The test statistic follows a StudentTDistribution[n-2] under ![]() :
:
In higher dimensions the test statistic follows a ChiSquareDistribution[r*s]:
For matrix comparisons the test statistic is invariant under affine transformations:
To test a particular value of Spearman's ![]() use CorrelationTest:
use CorrelationTest:
IndependenceTest can be used to select an appropriate test of independence:
SpearmanRankTest is one of the available tests:
SpearmanRankTest only detects monotonic dependence:
HoeffdingDTest can be used to detect a wider variety of dependence structures:
The Spearman rank test works with the values only when the input is a TimeSeries:
The Spearman rank test works with all the values together when the input is a TemporalData:
Related Guides
History
Text
Wolfram Research (2012), SpearmanRankTest, Wolfram Language function, https://reference.wolfram.com/language/ref/SpearmanRankTest.html.
CMS
Wolfram Language. 2012. "SpearmanRankTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SpearmanRankTest.html.
APA
Wolfram Language. (2012). SpearmanRankTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SpearmanRankTest.html
BibTeX
@misc{reference.wolfram_2025_spearmanranktest, author="Wolfram Research", title="{SpearmanRankTest}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/SpearmanRankTest.html}", note=[Accessed: 19-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_spearmanranktest, organization={Wolfram Research}, title={SpearmanRankTest}, year={2012}, url={https://reference.wolfram.com/language/ref/SpearmanRankTest.html}, note=[Accessed: 19-February-2026]}