PillaiTrace

PillaiTrace[m1,m2]

gives Pillai's trace for the matrices m1 and m2.

Details

  • PillaiTrace[m1,m2] gives Pillai's trace between m1 and m2.
  • Pillai's trace is a measure of linear dependence based on partitions of the pooled covariance matrix.
  • Pillai's trace is computed as Tr[TemplateBox[{{(, {Sigma, _, {(, 11, )}}, )}}, Inverse].Sigma_(12).TemplateBox[{{(, {Sigma, _, {(, 22, )}}, )}}, Inverse].Sigma_(21)] where 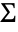is the covariance matrix of the pooled sample, which can be partitioned into 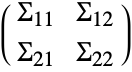where 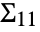and 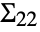correspond to the covariance matrices of the individual datasets.
  • The arguments m1 and m2 can be any real‐valued matrices or vectors of equal length.

Examples

open allclose all

Basic Examples  (3)

Compute Pillai's trace for two matrices:

Pillai's trace for two vectors:

Pillai's trace for a matrix and a vector:

Scope  (3)

Pillai's trace is typically used to detect linear dependence between random matrices:

Values tend to be near 1 for dependent matrices:

The value is much smaller for independent matrices:

Pillai's trace for machine-precision reals:

Use arbitrary precision:

Properties & Relations  (4)

Pillai's trace measures linear dependence:

Pillai's trace cannot detect nonlinear dependency:

HoeffdingD can be used to detect some nonlinear dependence structures:

Pillai's trace is asymptotically equivalent to WilksW:

Statistical significance can be tested using PillaiTraceTest:

Alternatively, use IndependenceTest to automatically choose a test:

Wolfram Research (2012), PillaiTrace, Wolfram Language function, https://reference.wolfram.com/language/ref/PillaiTrace.html.

Text

Wolfram Research (2012), PillaiTrace, Wolfram Language function, https://reference.wolfram.com/language/ref/PillaiTrace.html.

CMS

Wolfram Language. 2012. "PillaiTrace." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PillaiTrace.html.

APA

Wolfram Language. (2012). PillaiTrace. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PillaiTrace.html

BibTeX

@misc{reference.wolfram_2024_pillaitrace, author="Wolfram Research", title="{PillaiTrace}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/PillaiTrace.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_pillaitrace, organization={Wolfram Research}, title={PillaiTrace}, year={2012}, url={https://reference.wolfram.com/language/ref/PillaiTrace.html}, note=[Accessed: 14-November-2024 ]}