BlomqvistBeta[v1,v2]
gives Blomqvist's medial correlation coefficient β for the vectors v1 and v2.
gives Blomqvist's medial correlation coefficient β for the matrix m.
BlomqvistBeta[m1,m2]
gives Blomqvist's medial correlation coefficient β for the matrices m1 and m2.
BlomqvistBeta[dist]
gives the medial correlation coefficient matrix for the multivariate symbolic distribution dist.
BlomqvistBeta[dist,i,j]
gives the (i,j)![]() medial correlation coefficient for the multivariate symbolic distribution dist.
medial correlation coefficient for the multivariate symbolic distribution dist.


BlomqvistBeta
BlomqvistBeta[v1,v2]
gives Blomqvist's medial correlation coefficient β for the vectors v1 and v2.
gives Blomqvist's medial correlation coefficient β for the matrix m.
BlomqvistBeta[m1,m2]
gives Blomqvist's medial correlation coefficient β for the matrices m1 and m2.
BlomqvistBeta[dist]
gives the medial correlation coefficient matrix for the multivariate symbolic distribution dist.
BlomqvistBeta[dist,i,j]
gives the (i,j)![]() medial correlation coefficient for the multivariate symbolic distribution dist.
medial correlation coefficient for the multivariate symbolic distribution dist.
Details

- BlomqvistBeta[v1,v2] gives Blomqvist's medial correlation coefficient β between v1 and v2.
- Blomqvist's β between vectors x and y is given by Correlation[Sign[x-μx],Sign[y-μy]], where μx and μy are the medians of x and y, respectively.
- The arguments v1 and v2 can be any real‐valued vectors of equal length.
- For a matrix m with
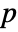 columns BlomqvistBeta[m] is a
columns BlomqvistBeta[m] is a 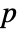 ×
×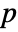 matrix of the β's between columns of m.
matrix of the β's between columns of m. - For an
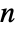 ×
×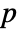 matrix m1 and an
matrix m1 and an 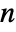 ×
×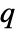 matrix m2 BlomqvistBeta[m1,m2] is a
matrix m2 BlomqvistBeta[m1,m2] is a 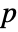 ×
×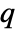 matrix of the β's between columns of m1 and columns of m2.
matrix of the β's between columns of m1 and columns of m2. - BlomqvistBeta[dist,i,j] is Probability[(x-μx)(y-μy)>0,{x,y}disti,j]-Probability[(x-μx)(y-μy)<0,{x,y}disti,j] where disti,j is the
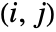
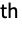 marginal of dist.
marginal of dist. - BlomqvistBeta is not well defined for discrete distributions or in the presence of ties.
- BlomqvistBeta[dist] gives a matrix β where the
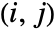
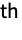 entry is given by BlomqvistBeta[dist,i,j].
entry is given by BlomqvistBeta[dist,i,j].
Examples
open all close allBasic Examples (4)
Scope (7)
Data (4)
Exact input yields exact output:
Approximate input yields approximate output:
SparseArray data can be used:
Applications (3)
Blomqvist's β is typically used to detect linear dependence between two vectors:
The absolute magnitude of β tends to 1 given strong linear dependence:
The value tends to 0 for linearly independent vectors:
Blomqvist's β can be used to measure linear association:
Blomqvist's β only detects monotonic dependence structures:
HoeffdingD can be used for a variety of other dependence structures:
Properties & Relations (7)
Blomqvist's β ranges from ![]() to
to ![]() for high negative and high positive association, respectively:
for high negative and high positive association, respectively:
Blomqvist's β matrix is symmetric:
The diagonal elements of Blomqvist's β matrix are 1:
Blomqvist's ![]() for even sample sizes:
for even sample sizes:
Count the number of points in each quadrant:
Blomqvist's β will yield ![]() or
or ![]() if there is perfect monotonic association:
if there is perfect monotonic association:
This is in contrast to Correlation, which measures the degree of linear association:
BlomqvistBetaTest can be used to test the value of β:
IndependenceTest can be used to automatically select an appropriate test:
Related Guides
History
Text
Wolfram Research (2012), BlomqvistBeta, Wolfram Language function, https://reference.wolfram.com/language/ref/BlomqvistBeta.html.
CMS
Wolfram Language. 2012. "BlomqvistBeta." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BlomqvistBeta.html.
APA
Wolfram Language. (2012). BlomqvistBeta. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BlomqvistBeta.html
BibTeX
@misc{reference.wolfram_2025_blomqvistbeta, author="Wolfram Research", title="{BlomqvistBeta}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/BlomqvistBeta.html}", note=[Accessed: 20-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_blomqvistbeta, organization={Wolfram Research}, title={BlomqvistBeta}, year={2012}, url={https://reference.wolfram.com/language/ref/BlomqvistBeta.html}, note=[Accessed: 20-January-2026]}