GoodmanKruskalGamma[v1,v2]
gives the Goodman–Kruskal ![]() coefficient for the vectors v1 and v2.
coefficient for the vectors v1 and v2.
gives the Goodman–Kruskal ![]() coefficients for the matrix m.
coefficients for the matrix m.
GoodmanKruskalGamma[m1,m2]
gives the Goodman–Kruskal ![]() coefficients for the matrices m1 and m2.
coefficients for the matrices m1 and m2.
GoodmanKruskalGamma[dist]
gives the ![]() coefficient matrix for the multivariate symbolic distribution dist.
coefficient matrix for the multivariate symbolic distribution dist.
GoodmanKruskalGamma[dist,i,j]
gives the ![]()
![]()
![]() coefficient for the multivariate symbolic distribution dist.
coefficient for the multivariate symbolic distribution dist.


GoodmanKruskalGamma
GoodmanKruskalGamma[v1,v2]
gives the Goodman–Kruskal ![]() coefficient for the vectors v1 and v2.
coefficient for the vectors v1 and v2.
gives the Goodman–Kruskal ![]() coefficients for the matrix m.
coefficients for the matrix m.
GoodmanKruskalGamma[m1,m2]
gives the Goodman–Kruskal ![]() coefficients for the matrices m1 and m2.
coefficients for the matrices m1 and m2.
GoodmanKruskalGamma[dist]
gives the ![]() coefficient matrix for the multivariate symbolic distribution dist.
coefficient matrix for the multivariate symbolic distribution dist.
GoodmanKruskalGamma[dist,i,j]
gives the ![]()
![]()
![]() coefficient for the multivariate symbolic distribution dist.
coefficient for the multivariate symbolic distribution dist.
Details

- GoodmanKruskalGamma[v1,v2] gives the Goodman–Kruskal coefficient
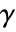 between v1 and v2.
between v1 and v2. - Goodman–Kruskal
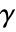 is a measure of monotonic association based on the relative order of consecutive elements in the two lists.
is a measure of monotonic association based on the relative order of consecutive elements in the two lists. - Goodman–Kruskal
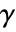 between
between 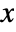 and
and 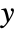 is given by
is given by 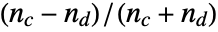 , where
, where 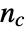 is the number of concordant pairs of observations and
is the number of concordant pairs of observations and 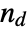 is the number of discordant pairs.
is the number of discordant pairs. - A concordant pair of observations
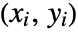 and
and 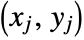 is one such that both
is one such that both 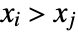 and
and 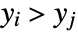 or both
or both 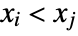 and
and 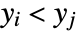 . A discordant pair of observations is one such that
. A discordant pair of observations is one such that 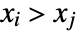 and
and 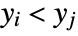 or
or 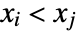 and
and 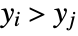 .
. - If no ties are present,
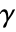 is equivalent to KendallTau.
is equivalent to KendallTau. - The arguments v1 and v2 can be any real‐valued vectors of equal length.
- For a matrix m with
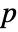 columns, GoodmanKruskalGamma[m] is a
columns, GoodmanKruskalGamma[m] is a 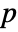 ×
×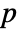 matrix of the
matrix of the 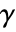 -coefficients between columns of m.
-coefficients between columns of m. - For an
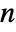 ×
×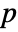 matrix m1 and an
matrix m1 and an 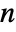 ×
×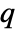 matrix m2, GoodmanKruskalGamma[m1,m2] is a
matrix m2, GoodmanKruskalGamma[m1,m2] is a 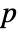 ×
×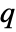 matrix of the
matrix of the 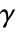 -coefficients between columns of m1 and columns of m2.
-coefficients between columns of m1 and columns of m2. - GoodmanKruskalGamma[dist,i,j] gives
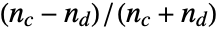 where
where 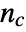 is equal to Probability[(x1-x2)(y1-y2)>0,{{x1,y1}disti,j,{x2,y2}disti,j}] and
is equal to Probability[(x1-x2)(y1-y2)>0,{{x1,y1}disti,j,{x2,y2}disti,j}] and 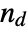 is equal to Probability[(x1-x2)(y1-y2)<0,{{x1,y1}disti,j,{x2,y2}disti,j}] where disti,j is the
is equal to Probability[(x1-x2)(y1-y2)<0,{{x1,y1}disti,j,{x2,y2}disti,j}] where disti,j is the 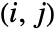
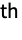 marginal of dist.
marginal of dist. - GoodmanKruskalGamma[dist] gives a matrix
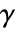 where the
where the 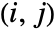
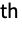 entry is given by GoodmanKruskalGamma[dist,i,j].
entry is given by GoodmanKruskalGamma[dist,i,j].
Examples
open all close allBasic Examples (4)
Scope (7)
Data (4)
Exact input yields exact output:
Approximate input yields approximate output:
SparseArray data can be used:
Applications (3)
Goodman–Kruskal ![]() is typically used to detect linear dependence between two vectors:
is typically used to detect linear dependence between two vectors:
The absolute magnitude of ![]() tends to 1 given strong linear dependence:
tends to 1 given strong linear dependence:
The value tends to 0 for linearly independent vectors:
Goodman–Kruskal ![]() measures linear association:
measures linear association:
Goodman–Kruskal ![]() can only detect monotonic dependency:
can only detect monotonic dependency:
HoeffdingD can be used to detect other dependence structures:
Properties & Relations (5)
Goodman–Kruskal ![]() ranges from -1 to 1 for negative and positive association, respectively:
ranges from -1 to 1 for negative and positive association, respectively:
The Goodman-Kruskal ![]() matrix is symmetric:
matrix is symmetric:
The diagonal elements of the Goodman–Kruskal ![]() matrix are 1:
matrix are 1:
In the absence of ties, Goodman–Kruskal ![]() is equivalent to KendallTau:
is equivalent to KendallTau:
Related Guides
History
Text
Wolfram Research (2012), GoodmanKruskalGamma, Wolfram Language function, https://reference.wolfram.com/language/ref/GoodmanKruskalGamma.html.
CMS
Wolfram Language. 2012. "GoodmanKruskalGamma." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GoodmanKruskalGamma.html.
APA
Wolfram Language. (2012). GoodmanKruskalGamma. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GoodmanKruskalGamma.html
BibTeX
@misc{reference.wolfram_2025_goodmankruskalgamma, author="Wolfram Research", title="{GoodmanKruskalGamma}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/GoodmanKruskalGamma.html}", note=[Accessed: 27-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_goodmankruskalgamma, organization={Wolfram Research}, title={GoodmanKruskalGamma}, year={2012}, url={https://reference.wolfram.com/language/ref/GoodmanKruskalGamma.html}, note=[Accessed: 27-February-2026]}