NumericalCalculus`
NumericalCalculus`

NLimit

NLimit[expr,z->z0]

numerically finds the limiting value of expr as z approaches z0.

Details and Options

  • To use NLimit, you first need to load the Numerical Calculus Package using Needs["NumericalCalculus`"].
  • The expression expr must be numeric when its argument z is numeric.
  • NLimit constructs a sequence of values that approach the point z0 and uses extrapolation to find the limit.
  • NLimit is unable to recognize small numbers that should in fact be zero. Chop may be needed to eliminate these spurious residuals.
  • NLimit often fails when the limit has a power law approach to infinity.
  • The following options can be given:
  • WorkingPrecisionMachinePrecisionprecision to use in internal computations
    DirectionAutomaticvector giving the direction of approach
    Scale1initial step size in the sequence of steps
    Terms7number of terms used to evaluate the limit
    MethodEulerSumthe method used to evaluate the result
    WynnDegree1degree used in Wynn's epsilon algorithm
  • The option Direction->d specifies that the approach vector to a finite limit point z0 is given by the complex number d. The default setting Direction->Automatic is equivalent to Direction->-1, and computes the limit as z approaches z0 from larger values.
  • NLimit approaches infinite limit points on a ray from the origin.
  • The option Scale specifies the initial step in the constructed sequence.
  • For finite limit points x0, the initial step is a distance Scale away from x0. For infinite limit points, the initial step is a distance Scale away from the origin.
  • The accuracy of the result is generally improved by increasing the number of terms, although increased WorkingPrecision will also usually be necessary.
  • Possible settings for Method include:
  • EulerSumconverts sequence to a sum and uses EulerSum
    SequenceLimituses SequenceLimit on constructed sequence
  • The option WynnDegree specifies the number of iterations of Wynn's epsilon algorithm to be used by SequenceLimit. In general, there must be at least 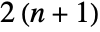terms for 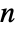iterations.

Examples

open allclose all

Basic Examples  (2)

Find the limit at zero:

Find the limit at infinity:

Scope  (2)

The expression can be manifestly complex:

The limit point can be complex:

Options  (8)

Terms  (2)

Expressions that approach their limiting value exponentially need fewer terms:

Increasing the number of terms can improve accuracy:

Error in numerical approximation:

Use more terms to reduce error:

Scale  (1)

Use Scale to avoid regions where the expression is undefined:

The function diverges for , so choose the initial step to avoid this divergence:

Direction  (1)

Approach 0 along the negative real axis (z can be input using zco):

Approach 0 along the positive imaginary axis:

Approach 0 from the 3^(rd) quadrant, 225°:

Method  (2)

An example where the default method works fairly well:

Using SequenceLimit produces poorer results:

An example where the default method works poorly:

Here, SequenceLimit produces the correct result:

WynnDegree  (1)

When using Method->SequenceLimit, increasing WynnDegree may improve the accuracy of the limit:

Error with WynnDegree->1:

Error with WynnDegree->3:

WorkingPrecision  (1)

Increasing WorkingPrecision alone does not produce a more accurate result:

Error with WorkingPrecision->20:

Error with WorkingPrecision->30:

To improve accuracy, the number of terms needs to be increased:

Applications  (2)

Find the limit of a numerically defined function:

Limits where parts of the expression have essential singularities:

In this case, the exact limit can be found:

Check:

Properties & Relations  (1)

SequenceLimit can be used directly to compute limits:

Possible Issues  (1)

Limits whose value approaches infinity are sometimes unable to be computed: