NumericalCalculus`
NumericalCalculus`

NLimit

NLimit[expr,z->z0]

z が z0に近付く際の expr の極限値を数値的に求める．

詳細とオプション

  • NLimitを使うためには，まず数値計算パッケージをロードしなくてはならない．それにはNeeds["NumericalCalculus`"]を実行する必要がある．
  • 式 expr は，その引数 z が数値である場合は，数値でなければならない．
  • NLimitは極限を求めるために点 z0に接近する値の列を構築し，外挿を使う．
  • NLimitは実際にはゼロとなるような小さい数を識別することができない．このような誤りの残余を排除するためにChopを使う必要があることがある．
  • 極限がベキ法則的に無限に近付く場合，NLimitは失敗することがよくある．
  • 次のオプションを与えることができる：
  • WorkingPrecisionMachinePrecision内部計算で使用する精度
    DirectionAutomatic接近の方向を与えるベクトル
    Scale1ステップ列の最初の刻み幅
    Terms7極限の評価に使用する項の数
    MethodEulerSum結果の評価に使用するメソッド
    WynnDegree1ウィン(Wynn)のイプシロン法で使用する次数
  • オプションDirection->d は，有限の極限点 z0 への接近ベクトルが複素数 d で与えられることを指定する．デフォルト設定のDirection->AutomaticはDirection->-1と等価であり，z が大きい値から z0に近付くときの極限を計算する．
  • NLimitは原点からの放射線上で無限の極限点に近付く．
  • オプションScaleは構築された列の最初のステップを指定する．
  • 有限極限点 x0 では，初期ステップは x0 から距離Scaleだけ離れたところである．無限極限点では，原点から距離Scaleだけ離れたところである．
  • 結果の正確さは通常項の数を増やすことで改善される．しかし通常WorkingPrecisionを増やすことも必要である．
  • Methodに可能な設定は以下の通りである：
  • EulerSum列を総和に変換し，EulerSumを使う
    SequenceLimit構築された列にSequenceLimitを使う
  • オプションWynnDegreeは，SequenceLimitで使われるウィンのイプシロン法の反復回数を指定する．一般に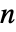， 回の反復に対しては少なくとも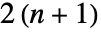個の項がなければならない．

例題

すべて開くすべて閉じる

例  (2)

ゼロにおける極限を見付ける：

無限で極限を探す：

スコープ  (2)

式は明らかに複素数であってもよい：

極限点は複素数のこともある：

オプション  (8)

Terms  (2)

極限値に指数関数的に接近する式にはもっと少ない項しか必要ない：

項の数を増やすと，確度が改善される場合がある：

数値近似の誤差：

誤差を減らすために項の数を増やす：

Scale  (1)

Scaleを使って，式が未定義である領域を避ける：

関数 は のとき分岐するので，この分岐を避けるために初期ステップを選ぶ：

Direction  (1)

負の実軸に沿って0に接近する（zはzcoを使って入力することができる）：

正の虚軸に沿って0に接近する：

第三象限の225°から0に接近する：

Method  (2)

デフォルトメソッドがうまく使える例である：

SequenceLimitを使うと，結果が思わしくない：

デフォルトメソッドではあまりうまくいかない例：

ここではSequenceLimitを使うと正しい解が得られる：

WynnDegree  (1)

Method->SequenceLimitを使うときに，WynnDegreeを増加すると極限の確度が改善されることがある：

WynnDegree->1での誤差：

WynnDegree->3での誤差：

WorkingPrecision  (1)

WorkingPrecisionだけを増やしてもより正確な結果が出るわけではない：

WorkingPrecision->20での誤差：

WorkingPrecision->30での誤差：

確度を改善するためには，項の数を増やす必要がある：

アプリケーション  (2)

数値的に定義された関数の極限を見付ける：

式の一部に真性特異点がある極限：

この場合，厳密な極限を見付けることができる：

検証する：

特性と関係  (1)

極限を計算するためにSequenceLimitを直接使うことができる：

考えられる問題  (1)

値が無限に近付くような極限は，計算できないこともある：