NumericalDifferentialEquationAnalysis`
NumericalDifferentialEquationAnalysis`

GaussianQuadratureWeights

GaussianQuadratureWeights[n,a,b]

a から b の区間における基本的な n 点ガウス求積法の n 個のペア{xi,wi}のリストを返す．ここで wi は横座標 xi の重みである．

GaussianQuadratureWeights[n,a,b,prec]

prec 桁精度で結果を返す．

詳細とオプション

  • GaussianQuadratureWeightsを使うためには，まず微分方程式の数値解析パッケージをロードしなくてはならない．それにはNeeds["NumericalDifferentialEquationAnalysis`"]を実行する必要がある．
  • ガウス求積法では，最適な横座標 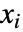において評価された被積分関数の値の線形結合として積分の値を近似す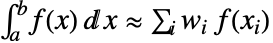る．である．
  • 横座標は，求積法が次数2n-1までのすべての多項式について厳密であるという意味で最適である．

例題

特性と関係  (1)

区間が0から1のとき，NIntegrate`GaussRuleDataはGaussianQuadratureWeightsと同じ横軸と重みを与える：

区間が0から1ではないときでも，NIntegrate`GaussRuleDataの結果をスケールすると，GaussianQuadratureWeightsと同じ結果になる：