NumericalDifferentialEquationAnalysis`
NumericalDifferentialEquationAnalysis`

GaussianQuadratureWeights

GaussianQuadratureWeights[n,a,b]

gives a list of the n pairs {xi,wi} of the elementary n-point Gaussian formula for quadrature on the interval a to b, where wi is the weight of the abscissa xi.

GaussianQuadratureWeights[n,a,b,prec]

attempts to give a result with prec digits of precision.

Details and Options

  • To use GaussianQuadratureWeights, you first need to load the Numerical Differential Equation Analysis Package using Needs["NumericalDifferentialEquationAnalysis`"].
  • Gaussian quadrature approximates the value of an integral as a linear combination of values of the integrand evaluated at optimal abscissas : .
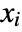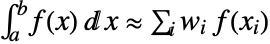  • The abscissas are optimal in the sense that the quadrature formula is exact for all polynomials up to degree 2n-1.

Examples

Properties & Relations  (1)

NIntegrate`GaussRuleData gives the same abscissas and weights as GaussianQuadratureWeights when the interval is from 0 to 1:

If the interval range is different from 0 to 1, scaling the result of NIntegrate`GaussRuleData also gives the same result as GaussianQuadratureWeights: