Acoustic Mirror

Introduction	Initial and Boundary Conditions
Pressure Acoustics Model	Solve the PDE Model
Domain	Post-processing and Visualization
Sound Source	Nomenclature
Mesh Generation	References

Introduction

An acoustic mirror is a passive device that collects and amplifies the sound waves. They are often designed in a parabolic-shape made of sound hard materials, which allows them to reflect and focus incident sound signals. Before the invention of the radar system, acoustic mirrors were used to detects incoming aircraft. In recent years, due to its simple setup and their efficiency in the signal processing [1], acoustic mirrors are commonly used in aeroacoustic wind tunnels for noise measurement.

This study is to simulate the sound propagation across the paired sound mirrors. To visualize the scattering and refocusing patterns of the inharmonic sound signal, the acoustic PDE model is constructed in the time domain. However, with the usage of the Fourier transform we can quantify the performance of the mirrors in both the time and frequency domain. The modeling process also demonstrates the techniques on mesh refinement and the setup of sound sources.

The symbols and corresponding units used throughout this tutorial are summarized in the Nomenclature section.

Please refer to the information provided in "Acoustics in the Time Domain" for more general theoretical background for acoustics.

Load the finite element package.

Pressure Acoustics Model

In this example the propagation of sound waves can be described by the wave equation (2):

Define the variables and select the parameters for a time domain acoustics model.

Air is used as the sound medium.

Define material parameters for the time domain acoustics model.

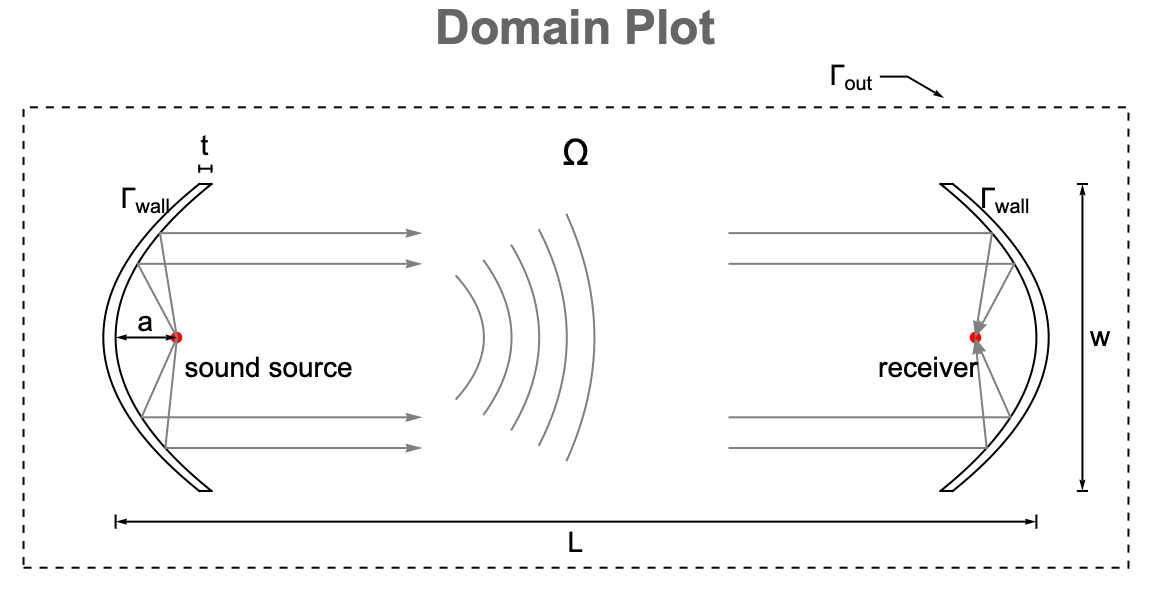
Domain

In the geometric model a pair of parabolic sound mirrors is installed at and . Each mirror is designed to have a width and a focal length . At the focus of the left parabolic mirror a there is a monopole sound source. At the focus of the right parabolic mirror there is a receiver.

When the input signal originates from the left focus, the sound wave reflects off the left mirror and propagates to the direction the mirror is pointing, sending the sound signal across to the paired mirror. The incoming wave then reaches the right mirror, which reflects and refocuses the signal toward the receiver.

Specify the parameters of the geometry.

Define the simulation domain

Subtracting the paired sound mirrors from a 2D rectangular domain specifies the simulation domain . In the domain plot the solid lines denote wall boundaries modeling the surface of the mirrors, and the dashed lines models an outlet boundary where the waves leave the domain.

Sound Source

In this model a point monopole source is placed on the left focus, and a Gaussian derivative pulse is used as the time-inharmonic sound input. As will be shown in the next section, a Gaussian derivative pulse has a smooth and bounded frequency spectrum, which makes it a favorable source signal for the analytical purpose.

Setup an input sound signal

with a half pulse width

As explained in the acoustics time domain tutorial, a monopole source term is written as:

where is a regularized Dirac delta function at the source location .

Set up the regularized delta functions

Set the source location for the monopole source

Mesh Generation

In acoustics simulations the wavelength of a sound wave needs to be resolved by a sufficiently fine mesh in order to get an accurate numerical solution. Here we set the max edge length to 3 nodes per , which means that there will be at least three elements per wavelength in each direction of the wave propagation:

For the time-harmonic wave the calculation of is straightforward. However, for the time-inharmonic wave that contains multiple frequencies, the wavelength in (3) is not explicitly specified. The rule to determine the mesh size is to ensure that each frequency components is well resolved, which poses the following constrain:

A common way to find the maximal frequency is to convert the input signal into the frequency domain with the Fourier transform.

Convert the input sound signal with a Fourier transform and visualize the frequency spectrum.

It is seen that the input signal is mostly constrained in the frequency range . The maximal frequency to resolve is then chosen to be .

Set the maximal resolving frequency

and the corresponding mesh size

Discretize the domain

Initial and Boundary Conditions

Since the sound signal begins with an undisturbed domain, the initial sound pressure and its derivative are set to zero.

Set the initial conditions for the silent domain.

There are two types of the boundary conditions involved in this example. On the outer boundary an absorbing boundary condition is specified to model the outgoing sound wave.

Set an absorbing boundary condition on the outer boundary.

On the wall boundary of the sound mirror a default sound hard boundary conditions is implicitly used.

Solve the PDE Model

To study the full process of the wave scattering and refocusing by the sound mirror, the simulation time is set to . The PDE model is solve numerically with NDSolveValue using the finite element method

Define the simulation end time.

Setup the PDE.

Evaluating this simulation will require a larger then typical amount of RAM memory. Evaluating the simulation on a computer with insufficient memory will not work.

Solve the PDE and monitor the time/memory usage.

Post-processing and Visualization

Sound Pressure Distribution

To analyze the effect of the sound mirror, we first visualize the sound propagation in the time domain.

Find the minimum and maximum sound pressure

on grids, and set the legend bar and ContourPlot options.

Visualize the sound wave propagation between the paired sound mirrors.

See this note about improving the visual quality of the animation.

At first, the monopole source on the left focus radiates sound waves in all directions. The left part of the wave hits the mirror and is then reflected to form the right-going plane wave. As the wave reaches the right mirror, it is reflected once more and concentrated toward the receiver.

To quantify the performance of the acoustic mirror, the sound pressure level at the receiver can be compared with the case without the mirror, that is, the free-space scattering wave.

First, we have to determine the traveling time of the sound signal in both cases. For the free-space propagating wave, the time to reach the receiver is simply calculated by . In the case with acoustic mirrors, however, the traveling time of the refocusing signal is extended due to the reflection, which is given by .

Calculate the time of arrival for the sound signals.

With the traveling time computed the pressure field of the free-space scattering wave [4] can be calculated analytically by:

Here denotes the input signal and represents the distance between the sound source and the receiver.

Calculate the sound pressure level at the receiver without the acoustic mirror.

Compare the sound signals received at the right focus.

The sound signal is better preserved by the acoustic mirror (blue line) in comparison with the case without a mirror (orange line). The effectiveness of the mirror can be further enhanced by widening the width of the mirror.

Next we quantify the mirror performance by calculating the amplification ratio: , where stands for the maximum sound pressure of the signal.

Calculate the amplification ratio of the sound mirror. FindMinimum is given tolerance options appropriate for the errors in the PDE solution.

Compared to the free-space scattering wave, the sound signal with the acoustic mirror has been enhanced about 3 times at the receiver.

Sound Pressure Spectrum

Although the acoustic PDE model is constructed in the time domain to simulate the inharmonic sound input, it is still possible to study the effect of the acoustic mirrors in the frequency domain. To do so a discrete Fourier transform (DFT) is used to convert the transient sound signal into the frequency spectrum. By visualizing the distribution of the frequency components the performance of the acoustic mirror can be shown over the selected frequency range: .

To apply the DFT the acoustic signal is sampled into a discrete list of sound pressure values.

Set the sampling rate

and calculate the corresponding data length from the duration of the input pulse,

Extract the sound pressure data in the time domain.

As explained in a separate tutorial, the discrete Fourier transform generates Fourier coefficients with a corresponding frequency component . The frequency resolution of the Fourier transform is then given by .

Compute the frequency resolution

For the frequency range of , however, the data length results in a coarse resolution that is not applicable for analysis. To improve the frequency resolution, the time domain dataset is extended with zeros for . This method [5] is also known as "Zero Padding".

To achieve a frequency resolution of . The extended dataset should have a length of points.

Set the extended data length

of the dataset.

Apply the zero padding.

Convert the sound signal by the Fourier transform.

Set the table of frequency components.

Visualize the normalized amplitude spectrum of the sound signals.

With the acoustic mirror, the spectrum of the refocus sound wave has been squeezed toward the center around . That is, the acoustic mirror tends to preserve the central frequency components of the incoming signal but losing the ones with higher or lower frequencies. To increase the amplification on both end of the spectrum [6] a wider mirror can be used, and the curvature of the mirror can also be adjusted based on sound source location.

Nomenclature

Symbol	Description	Unit
ρ	density	[kg/m³]
c	speed of sound	[m/s]
p	sound pressure	[Pa]
t	time	[s]
X	position vector	[m]
F	optional dipole source	[N/m³]
Q	optional monopole source	[1/s²]
w	mirror width	[m]
a	focal length	[m]
L	separation distance	[m]
Γ_wall	wall boundary	N/A
Γ_out	far-field boundary	N/A
Ω	computational domain	N/A
Ω_rec	computational domain without mirrors	N/A
τ	half pulse width	[s]
X_s	sound source location	[m]
h	mesh spacing	[m]
λ	sound wavelength	[m]
f	sound wave frequency	[Hz]
ω	sound wave angular frequency	[rad/s]
t_free	traveling time of free-space signal	[s]
t_free	traveling time of refocusing signal	[s]
u_i	Fourier coefficient	N/A
f_i	frequency component	[Hz]
d f	frequency resolution	[Hz]

References

1. Ihlenburg, Frank. The Medium-Frequency Range in Computational Acoustics: Practical and Numerical Aspects. Journal of Computational Acoustics, Vol.11, No. 2 175-193, 2003.

2. Helfer, Martin. Sound Source Localisation with Acoustic Mirrors, 2009.

3. Lindsten, Fredrik. A remark on zero-padding for increased frequency resolution, 2010.

4. Russell, Daniel, Titlow, Joseph and Bemmen, Ya-Juan. Acoustic monopoles, dipoles and quadropoles: An experiment revisited. American Journal of Physics 67, 660, 1999.

Top