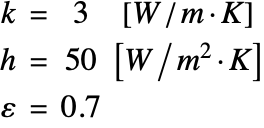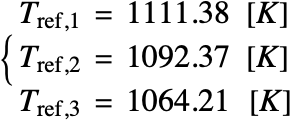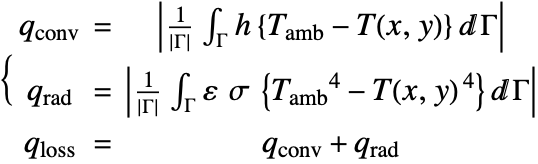Heat Transfer Model Verification Tests

Wolfram Language & System Documentation Center

Stationary Tests	Test Result Inspection
Transient Tests	References

This notebook contains tests that verify that the heat transfer partial differential equations (PDE) model works as expected. To run all tests, SelectAll and press Shift+Enter. The results will then be in the section Test Result Inspection.

Note that these tests can also serve as a basis for developing your own heat transfer models. As such, the tests are grouped into stationary (time-independent) and transient (time-dependent) tests. In both categories, one- and two-dimensional test models can be found.

In each test case, the visualization section is there to provide post-processing results for inspection; however, it is not a necessary part of the test. In the interest of saving runtime and reducing memory consumption, the cells in the visualization section are set to not be evaluatable. To make these cells evaluatable, select the cells in question, choose Cell ▶ Cell Properties and make sure "Evaluatable" is ticked.

The heat equation is used to solve for the temperature field in a heat transfer model. Please refer to the information provided in "Heat Transfer" for more general theoretical background for heat transfer analysis.

To avoid keeping memory-intensive previous results, set the history length to 0:

Stationary Tests

This section contains examples of stationary, which means non-time-dependent, heat transfer PDE models for the validation.

2D Single Equation

This section contains examples of a 2D stationary heat transfer PDE model with one equation.

HeatTransfer-FEM-Stationary-2D-Single-HeatTransfer-0001

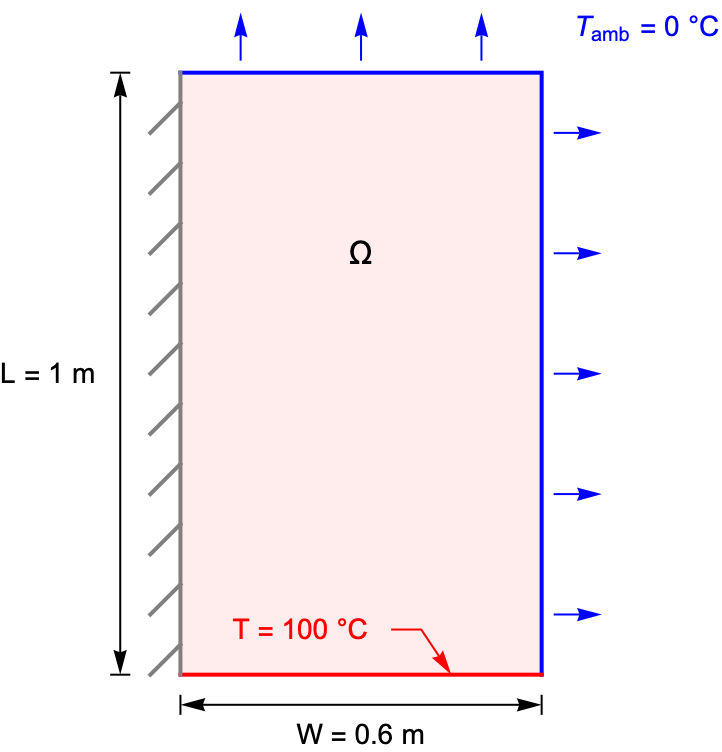
The following test case demonstrates a 2D stationary thermal analysis. The model domain is a rectangular region with a width of and a length of . At the lower boundary, the temperature is kept at , and the top and right boundaries are exposed to an ambient environment with a natural convection. The remaining left boundary is thermally insulated. The ambient temperature and the heat transfer coefficient are given by and , respectively.

Test Reference

[1] A. D. Cameron, J. A. Casey and G. B. Simpson. Benchmark Tests for Thermal Analysis. NAFEMS Documentation.

Equation

For a steady-state heat transfer model without sources, the transient term and the source term in the heat equation are set to zero. Since a solid is modeled, internal velocity also vanishes, and the heat equation simplifies to:

The heat transfer coefficient and the thermal conductivity of the medium are given by and , respectively. The ambient temperature is held at .

Define the model variables and parameters:

Set up a 2D steady-state heat transfer model:

Solution

At the point , the referenced solution [1] temperature value is given as .

Specify the reference temperature value at point

Boundary Conditions

The temperature at the lower boundary is fixed at .

Set up a temperature surface boundary condition on the lower boundary:

The top and right boundaries are exposed to the natural convection to the ambient environment at temperature .

Set up a convective boundary condition on the top and right boundaries:

A default thermal insulated boundary condition is implicitly applied on the remaining left boundary.

Region

Set up the model region:

Test 1

Solve the PDE model and monitor time/memory usage:

Test the inactive PDE:

Visualization

The following cells are marked as not evaluatable to save the runtime and memory consumed. To make these cells evaluatable, select the cells in question, choose Cell ▶ Cell Properties and make sure "Evaluatable" is ticked.

Set up a legend bar and ContourPlot options for the temperature field plot:

Visualize the temperature field:

HeatTransfer-FEM-Stationary-2D-Single-HeatTransfer-0002

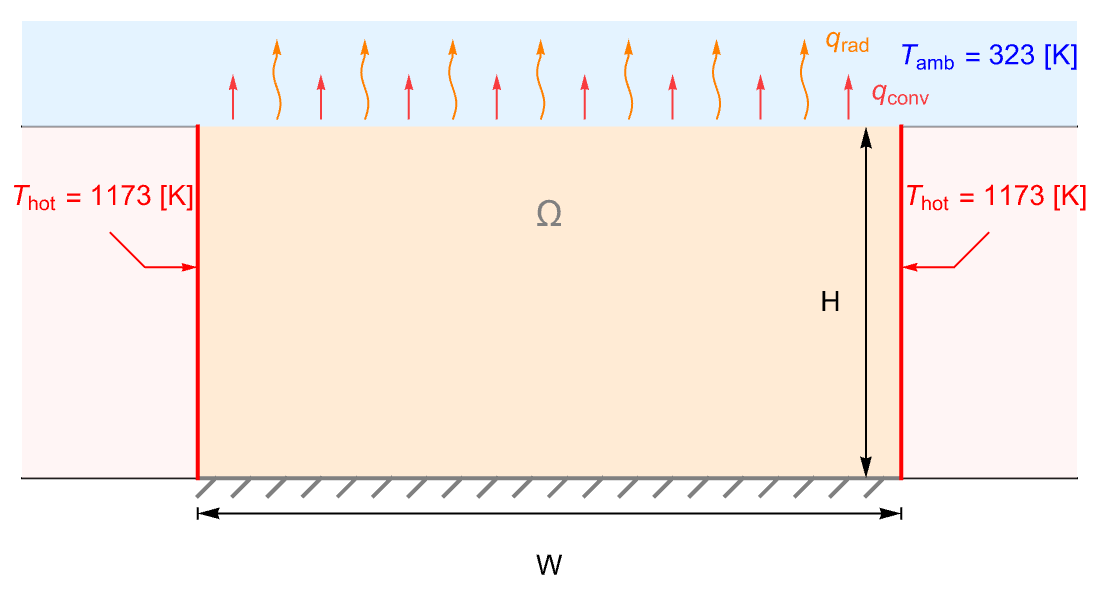
The following test case demonstrates a 2D stationary thermal analysis. The model domain is a ceramic strip that is embedded in a high-thermal-conductivity material.

The side boundaries of the strip are maintained at a constant temperature . The top surface of the strip is losing heat via both convection and radiation to the ambient environment at . The bottom boundary, however, is assumed to be thermally insulated.

Test Reference

[2] J. P. Holman, Heat Transfer Tenth Edition. McGraw-Hill, pp. 111, Example 3-10 (2008).

Equation

The thermal conductivity , heat transfer coefficient and emissivity of the ceramic strip are given by:

The temperature of the left and right boundaries is held at , and the ambient temperature remains at .

Define the model variables and parameters:

Set up a 2D steady-state heat transfer model:

Solution

At points , and , the referenced solution temperature values [3] are given by:

Specify the reference temperature value at points

and

Boundary Conditions

On the left and right boundaries, the temperature is held at .

Set up the temperature surface boundary condition at the left and right boundaries:

The top boundary is exposed to the environment ambient temperature , and loses heat by both thermal convection and radiation.

Set up the convective boundary condition with the heat transfer coefficient

Set up the thermal radiation boundary condition:

A default thermal insulated boundary condition is implicitly applied on the remaining bottom boundary.

Region

The ceramic strip has a width of and a height of .

Set up the model region:

Test 1

Solve the PDE model and monitor time/memory usage:

Verify the solution:

Visualization

The following cells are marked as not evaluatable to save runtime and memory consumed. To make these cells evaluatable, select the cells in question, choose Cell ▶ Cell Properties and make sure "Evaluatable" is ticked.

Set up a legend bar and ContourPlot options for the temperature field plot:

Visualize the temperature field:

Next, calculate the rate of heat loss at the top surface of the strip. The convection and radiation heat flux , are given by:

Calculate the rate of heat loss

at the top surface:

The heat loss rate of the ceramic strip is found as . This value can be checked by utilizing the law of energy conservation. That is, the total heat loss from the top surface must equal the conductive heat gain from the left and right boundaries:

Calculate the total heat gain

from side boundaries of the ceramic strip:

Note that the heat gain value matches the rate of heat loss .

2D Axisymmetric Single Equation

This section contains axisymmetric stationary heat transfer PDE model in cylindrical coordinates with one equation.

HeatTransfer-FEM-Stationary-2DAxisym-Single-HeatTransfer-0001

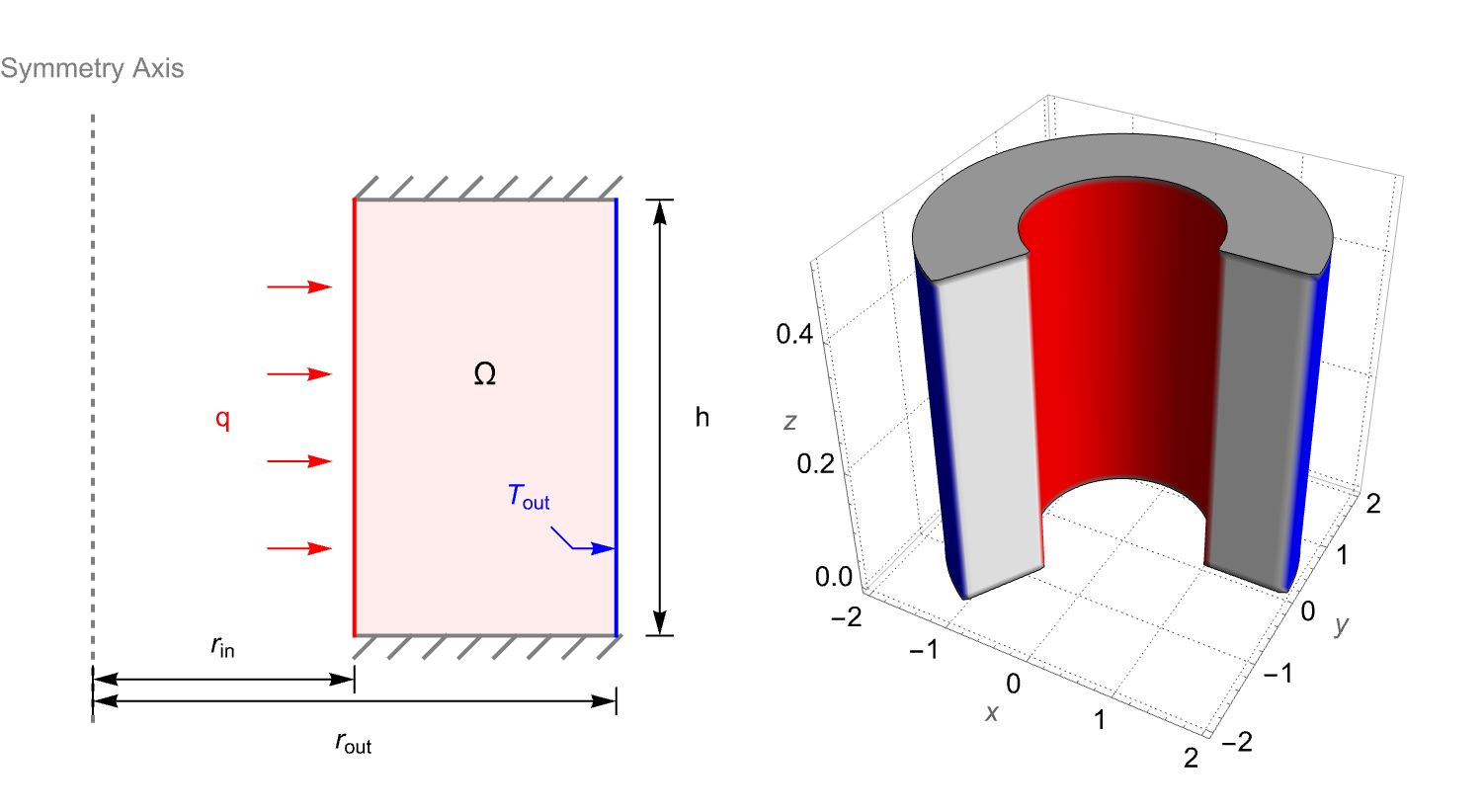
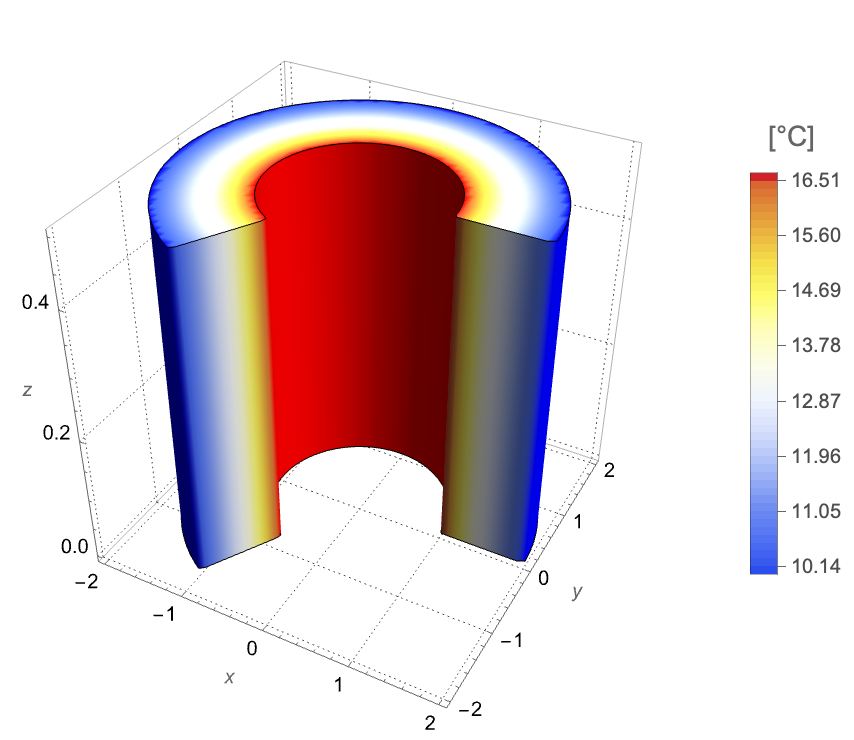
The following test case demonstrates a 2D axisymmetric steady-state thermal analysis. The model domain is a hollow cylinder with a height of . The inner radius and the outer radius are given by and , respectively. At the inner boundary, a constant heat flux is applied to heat the domain. On the outer boundary, the temperature is held at . The remaining bottom and top boundaries are thermally insulated.

Test Reference

[4] J. M. Owen and R. H. Rogers. Flow and Heat Transfer in Rotating-Disc Systems. Wiley, (1989).

Equation

For a 2D axisymmetric stationary heat transfer model without sources, the transient term and the source terms in the heat equation are set to zero. Since the medium is solid and the model is rotationally symmetric in the direction, the terms involving the flow velocity and the coordinate also vanish. Then the heat equation simplifies to:

Define the model variables and parameters. The material has a thermal conductivity

Set up a 2D steady-state heat transfer model:

Solution

The analytical solution of the temperature field is given by:

Set up the analytical solution for the temperature field in a hollow cylinder:

Boundary Conditions

The inner boundary is subjected to a constant inward heat flux .

Set up a heat flux boundary condition on the inner boundary:

The temperature at the outer boundary is fixed at .

Set up a temperature surface boundary condition on the outer boundary:

A default thermal insulated boundary condition is implicitly applied on the remaining bottom and top boundaries.

Region

Set up the model region:

Test 1

Solve the PDE model and monitor time/memory usage:

Test the inactive PDE:

Visualization

Set up a legend bar and ContourPlot options for the temperature field plot:

Visualize the temperature distribution in the radial direction:

Inspect the temperature field of the hollow cylinder:

Inspect the error at

Strictly speaking, this model could be simplified further, as there is no dependency of the solution, but the original benchmark formulation is used.

HeatTransfer-FEM-Stationary-2DAxisym-Single-HeatTransfer-0002

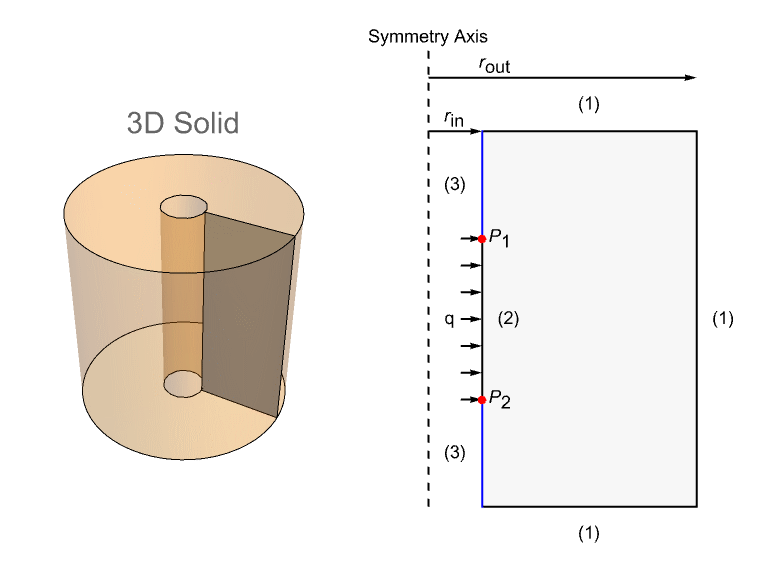
This section contains a model taken from a NAFEMS benchmark collection, which shows an axisymmetric steady-state thermal analysis. The model domain is a cross section of a 3D solid hollow cylinder with a height of . The inner radius and the outer radius are given by and , respectively. The model is set up with three different boundary conditions: a fixed temperature condition at the boundaries marked with (1), a prescribed heat flux at (2) and an insulation/symmetry at the remaining boundaries (3).

Test Reference

[5] A. D. Cameron, J. A. Casey and G. B. Simpson. Benchmark Tests for Thermal Analysis. NAFEMS Documentation.

Equation

For a 2D axisymmetric stationary heat transfer model without sources, the time derivative term and the source term in the heat equation are set to zero. Since the medium is solid and the model is rotationally symmetric in the direction, the terms involving the flow velocity and the axis also vanish. Then the heat equation simplifies to:

Define the model variables:

The material has a thermal conductivity .

Set up the material parameters:

Set up a 2D axisymmetric, steady-state heat transfer model:

Define the geometry parameters:

Here and are the heights of the points and , respectively.

Solution

The benchmark result for the target location is a temperature of .

Specify that the referenced solution temperature value is given by:

Boundary Conditions

The boundary is subjected to a constant inward heat flux .

Set up a heat flux boundary condition on the boundary:

The temperature at the boundaries is fixed at .

Set up a temperature surface boundary condition on the boundaries:

A default thermal insulated boundary condition is implicitly applied on the remaining boundaries .

Region

Set up the model region:

Test 1

Solve the PDE model and monitor time/memory usage:

Verify the solution of the PDE:

Inspect the error in percent:

Test 2

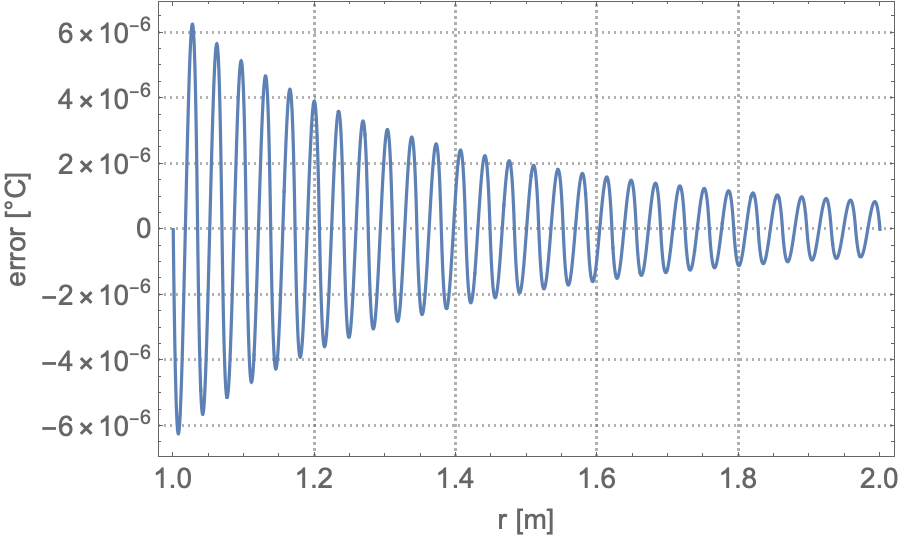
The solution obtained by the 2D axisymmetric approximation can be crosschecked with the solution from a 3D model.

Create the full 3D region:

Set up the 3D model:

Solve the full 3D model:

Since there is a symbolic description of the region, the option "ImproveBoundaryPosition" can be used for 3D geometries to further improve the boundary shape of the mesh.

Verify the solution of the PDE:

Inspect the error in percent:

Visualization

Visualize the temperature distribution with ContourPlot:

Inspect the temperature field of the hollow cylinder:

Transient Tests

This section contains examples of transient (time-dependent) heat transfer PDE models for validation.

1D Single Equation

This section contains examples of transient heat transfer ordinary differential equations (ODE) models with one equation. Ordinary differential equations with one independent variable are a special case of partial differential equations that usually deal with more than one independent variable.

HeatTransfer-FEM-Transient-1D-Single-HeatTransfer-0001

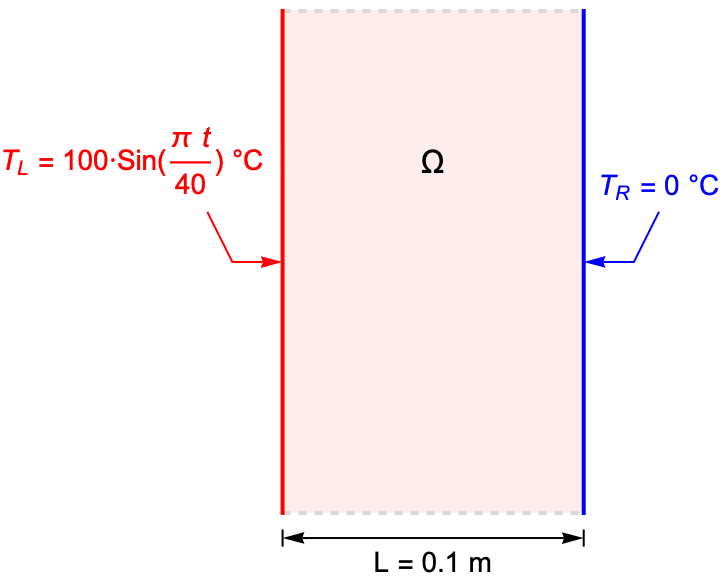
The following test case shows a transient heat diffusion process within a plate. The temperature on the left surface varies sinusoidally in time; on the other surface, the temperature is fixed at . It is assumed that the plate is very large compared to its thickness, so the analysis reduces to a 1D heat transfer model along the thickness.

Test Reference

[6] A. D. Cameron, J. A. Casey and G. B. Simpson. Benchmark Tests for Thermal Analysis. NAFEMS Documentation.

Equation

For a transient heat transfer model in a solid without sources, the source term and the internal velocity in the heat equation are set to zero. The heat equation then simplifies to:

The density, heat capacity and thermal conductivity of the medium are given by , and , respectively.

Define the model variables and parameters:

Set up a 1D transient heat transfer model:

Solution

At time , the referenced solution [1] of the temperature at point is given as .

Specify the reference temperature value at point

Boundary Conditions

On the left surface, the plate experiences a transient heating, where the temperature varies sinusoidally in time by . On the right surface, the temperature is held at .

Set up the temperature surface boundary condition on both ends of the domain:

Initial Conditions

At time , the temperature of the plate is .

Specify the initial condition:

Region

The thickness of the plate is given by .

Set up the model region:

Test 1

Set the simulation end time

Solve the PDE model and monitor time/memory usage:

Verify the solution of the PDE:

Visualization

Visualize the evolution of the temperature field within the plate:

HeatTransfer-FEM-Transient-1D-Single-HeatTransfer-0002

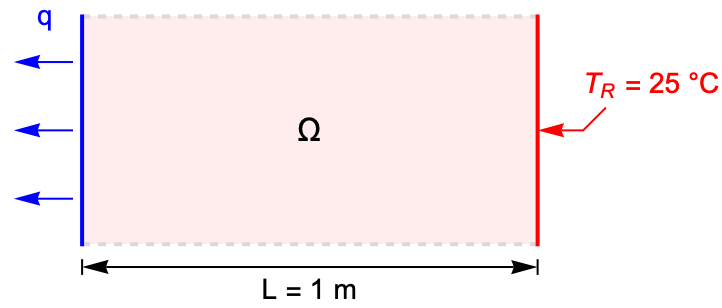
The following test case demonstrates a transient heat diffusion within a rod. On the left end, a constant outward heat flux is set to simulate the cooling process. On the right end, the temperature is fixed at .

Test Reference

[7] H. S. Carslaw and J. C. Jaeger. Conduction of Heat in Solids. Oxford at the Clarendon Press, 2nd ed. (1959).

Equation

For a transient heat transfer model in a solid without sources, the source term and the internal velocity in the heat equation are set to zero. The heat equation then simplifies to:

The density, heat capacity and thermal conductivity of the medium are given by , and , respectively.

Define the model variables and parameters:

Set up a 1D transient heat transfer model:

Solution

The analytical solution of the temperature field is given by:

Set up the analytical solution for the temperature field in the rod:

Boundary Conditions

The left end is losing heat at a constant outward heat flux .

Set up the heat flux boundary condition on the left end:

The temperature at the right end is fixed at .

Set up the temperature surface boundary condition on the right end:

Initial Conditions

At time , the temperature of the plate is .

Specify the initial condition:

Region

The model domain is a rod with a length of .

Set up the model region:

Test 1

Set the simulation end time

Solve the PDE model and monitor time/memory usage:

Verify the solution of the PDE:

Visualization

Visualize the evolution of the temperature field within the plate:

Inspect the error at

2D Axisymmetric Single Equation

This section contains an axisymmetric transient heat transfer PDE model in cylindrical coordinates with one equation.

HeatTransfer-FEM-Transient-2DAxisym-Single-HeatTransfer-0001

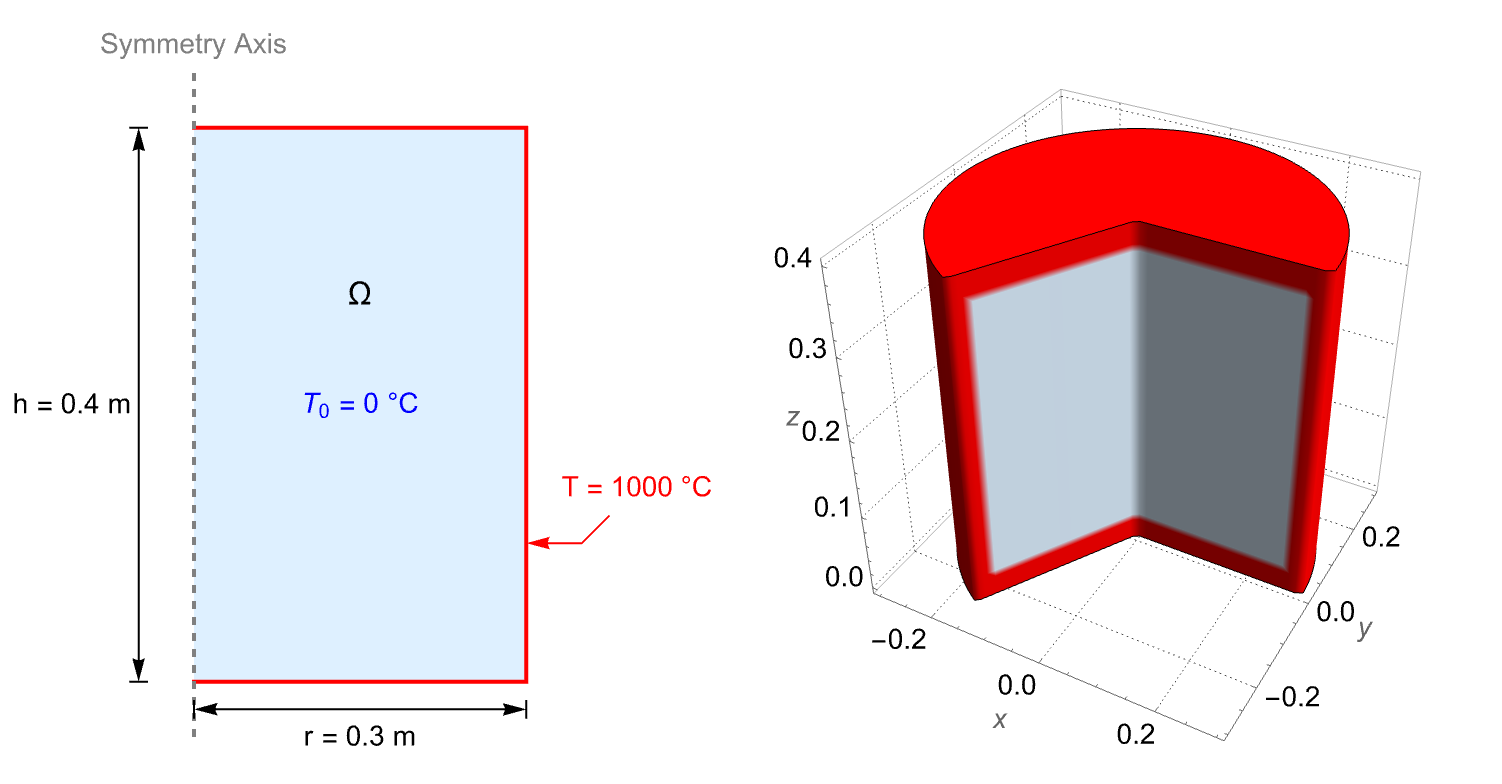
The following test case demonstrates a 2D axisymmetric transient thermal analysis. The model domain is a cylinder with a radius of and a height of . The temperature of the entire domain begins at . At the outer boundaries, the temperature experiences a step jump to and stays at for .

Test Reference

[8] A. D. Cameron, J. A. Casey and G. B. Simpson. Benchmark Tests for Thermal Analysis. NAFEMS Documentation.

Equation

When modeling the heat transfer in a solid medium without sources, the internal velocity and the source in the heat equation are set to zero. Since the model is rotationally symmetric in the direction, the terms involving the coordinate also vanish. Then the heat equation simplifies to: