固体力学モデル検証テスト

定常テストテスト結果の検査
固有モード解析

固体力学PDE成分は試験的な段階である．

このノートブックには，固体力学の偏微分方程式(PDE)モデルが想定通りに動作することを検証するテストが含まれている．すべてのテストを実行するためにはすべてを選択を選んでShift+Enterを押す．その結果はテスト結果の検査のセクションに表示される．

これらのテストは，自分の固体力学モデルを開発する基本としても役立つ．したがって，テストは定常（時間独立）テストと過渡（時間依存）テストにグループ化されている．どちらのグループにも二次元と三次元のテストがある．

どのテストにも可視化のセクションがあり，検査のための後処理の結果を提供するが，テストに必要な部分ではない．ランタイムを節約しメモリ使用量を削減するために，可視化セクションのセルは評価不可に設定してある．これらのセルを評価可にしたい場合は，該当のセルを選び，セル ▶ セルのプロパティを選んで「評価可能」にチェックマークを付ける．

固体力学方程式は荷重下での制約を受けた物体の変位について解くために使われる．固体力学解析の一般的な理論的背景は「固体力学」に記載されている情報をご参照いただきたい．

有限要素パッケージをロードする：
メモリ負荷の高い前の結果を保存しないように，履歴保存を0に設定する：
荷重下の構造の変形を可視化するヘルパー関数：

定常テスト

このセクションには検証のための定常（時間非依存）固体力学PDEモデルの例が含まれている．

2D方程式

このセクションには2Dの定常固体力学PDEモデルの例が含まれている．

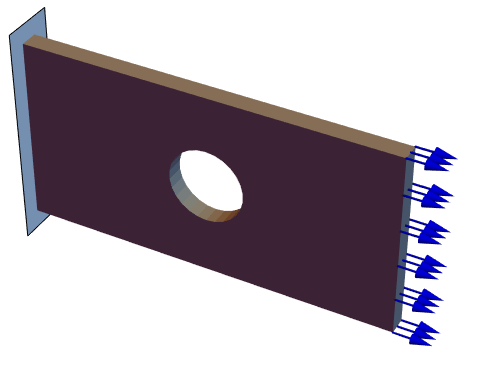
SolidMechanics-FEM-Stationary-2D-PlaneStress-0001

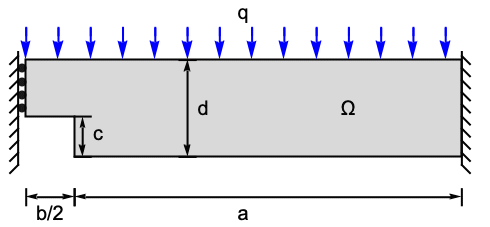
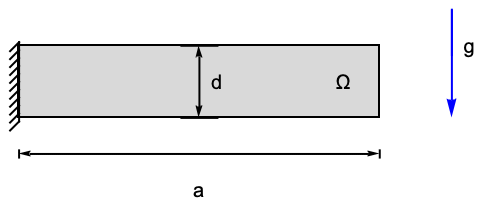
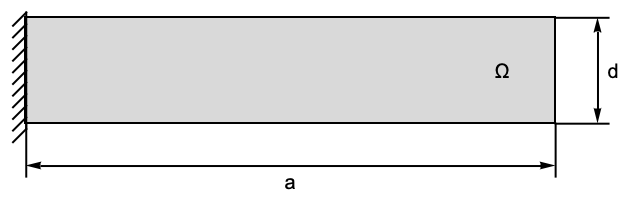
以下のテストは2D平面応力解析のさまざまな面を検証する．モデル領域は幅，高さ ，厚さ の切欠き梁である．左境界にはローラー拘束があり，構造は右端で固定されている．下向きの圧力 が上面に作用している．残りの境界は自由に動く．ヤング率は として，ポワソン比は として与えられる．

8.gif

テストの参照

M. Asghar Bhatti. Fundamental Finite Element Analysis and Applications. Wiley., Page 510, Example 7.7, Notched Beam

M. Asghar Bhatti. Fundamental Finite Element Analysis and Applications. Wiley. Supplementary examples from Book web page, Page 34, Chapter 7, Notched Beam

方程式

標準的な平面応力モデルを使う．

モデル変数とパラメータを定義する：
2Dの定常状態固体力学モデルを設定する：
応力関数とひずみ関数を使う2つ目の2D定常状態固体力学モデルを設定する：
解法

節点変位を与える．

基準節点変位を指定する：
境界条件

構造は右側で固定されている．

構造を右側で固定する：

構造は左側でy方向にローラーが付いている．

左側のy方向のローラー：

上部には下向きの50単位の圧力がかかる．

上部に作用する境界荷重を設定する：

残りの辺は自由に動く．

領域
モデル領域を設定する：
テスト1：
PDEモデルを解き，時間／メモリの使用量を監視する：
非アクティブなPDEをテストする：
テスト2
PDEモデルを解き，時間／メモリの使用量を監視する：
非アクティブなPDEをテストする：
テスト3
材料モデルを検証する：
テスト4
反力を計算する：
反力を検証する：
可視化

以下のセルはランタイムと消費メモリを節約するために評価不可にしてある．これらのセルを評価するためには，セルを選んでセル ▶ セルのプロパティを選び「評価可能」をチェックする．

変形した構造を可視化する：
コメント

バッティの例はさらに進んでさまざまな応力を計算する．バッティの例は線形要素だけに基づいている．しかしWolfram言語では，高次の補間を線形要素の場合にも使用するための特別な技法，および導関数を回復する特別なアルゴリズムが使われている．したがって，Wolfram言語で計算された応力値とバッティの単純（かつ有益）な例は合致しないが，ここでは示さない．

SolidMechanics-FEM-Stationary-2D-PlaneStress-0002

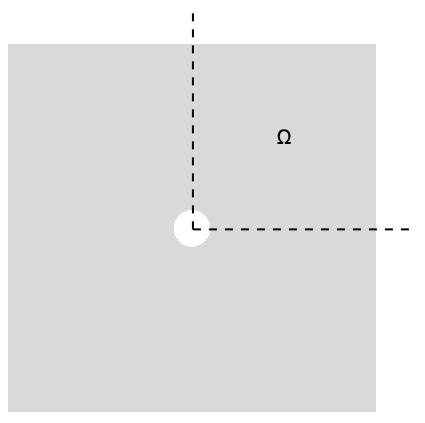
次のテストは2D平面応力解析を検証し，応力を計算して解析解と比較する．もとのモデルは内部に穴の開いた無限板である．モデルのシミュレーションを行うために，領域は有限にし，左下角に4分の1の穴の開いた矩形の板の4分の1対称である．

12.gif

モデル化された板は幅が ，高さも ，厚さが である．穴の半径は である．左境界には，構造が上下には動くが右には動けないようなローラー拘束がある．底には構造が左右には動くが上下には動かないようなローラー拘束がある．右側にはx方向に の圧力が働いている．残りの境界は自由に動く．ヤング率は必要ではなく が想定されており，ポワソン比は である．

20.gif

テストの参照

D. Roylance, Mechanics of Materials, Wiley., Page 184

方程式

標準的な平面応力モデルを使う．

モデルの変数とパラメータを定義する：
2D定常状態固体力学モデルを設定する：
応力とひずみの関数を使う2つ目の2D定常状態固体力学モデルを設定する：
解法

x方向の応力の式を与える．

基準の応力関数を値で指定する：
境界条件

構造は右側で固定されている．

底のy方向のローラー拘束：

構造は左側にy方向のローラーが付いている．

左側のx方向のローラー拘束：

右側では下向きの正のx方向に1000 [Pa]の圧力が作用している．

右側でx方向に作用する境界荷重を設定する：

残りの面は自由に動く．

領域
モデル領域を設定する：
テスト1
PDEモデルを解き，応力を計算する：
応力のPDEをテストする：
テスト2
PDEモデルを解き，調整されたメッシュの応力を計算する：
テスト3
PDEモデルを解き，応力を計算する：
非アクティブなPDEをテストする：
テスト4
PDEモデルを解き，応力を計算する：
非アクティブなPDEをテストする：
可視化

以下のセルはランタイムと消費メモリを節約するために評価不可にしてある．これらのセルを評価するためには，セルを選んでセル ▶ セルのプロパティを選び「評価可能」をチェックする．

解析応力と計算された応力をプロットする．
計算された応力の相対誤差率をプロットする．
コメント

最後の想定された逸脱以外，解析の結果とシミュレーションの結果はほぼ一致する．解析モデルはここでモデル化しなかった無限板のためのものなので，最後の部分の逸脱は想定されている．を設定して領域を拡大すると，解の質がさらに向上する．

SolidMechanics-FEM-Stationary-2D-PlaneStress-0003

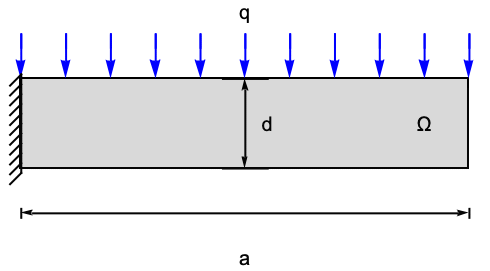
次のテストは，梁の2D平面応力解析を検証する．モデル領域は合計幅 ，高さ ，厚さ の梁である．梁は左境界で壁に固定されている．上部には下向きの圧力 が作用している．残りの境界は自由に動く．ヤング率は で与えられ，ポワソン比は である．質量密度はで与えられる．

30.gif

テストの参照

G. Backstrom, Simple displacement and Vibration, GB Publishing, 2006, ISBN: 9-1975553-20, Page 59

方程式

標準的な平面応力モデルを使う．

モデルの変数とパラメータを定義する：
2D定常状態固体力学モデルを設定する：
応力とひずみの関数を使う2番目の2D定常状態固体力学モデルを設定する：
解法

節点変位が与えられる．

基準の節点変位を指定する：
境界条件

構造は左側で固定されている．

左側で構造を固定する：

上部には下向きの10^6単位の圧力がかかる．

上部に作用する境界荷重を設定する：

残りの面は自由に動く．

領域
モデル領域を設定する：
テスト1
PDEモデルを解き，時間／メモリの使用量を監視する：
非アクティブなPDEをテストする：
テスト2
三角メッシュ上でPDEを解く：
非アクティブなPDEをテストする：
テスト3
PDEモデルを解き，時間／メモリの使用量を監視する：
非アクティブなPDEをテストする：
テスト4
PDEモデルを解き，時間／メモリの使用量を監視する：
非アクティブなPDEをテストする：
可視化

以下のセルはランタイムと消費メモリを節約するために評価不可にしてある．これらのセルを評価するためには，セルを選んでセル ▶ セルのプロパティを選び「評価可能」をチェックする．

変形した構造を可視化する：
垂直変位の解析解と数値解をプロットする：

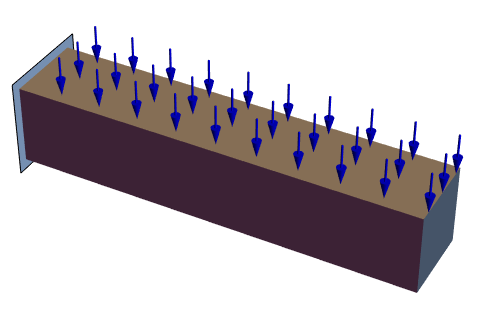
SolidMechanics-FEM-Stationary-2D-PlaneStress-0004

次のテストは梁の2D平面応力解析を検証する．モデル領域は合計幅が ，高さが ，厚さが の梁である．梁は左境界で壁に固定されている．残りの境界は自由に動く．物体には重量が作用する．ヤング率は で与えられ，ポワソン比は である．質量密度はで与えられる．

40.gif

テストの参照

G. Backstrom, Simple displacement and Vibration, GB Publishing, 2006, ISBN: 9-1975553-20, Page 68

方程式

標準的な平面応力モデルを使う．

モデルの変数とパラメータを定義する：
2D定常状態固体力学モデルを設定する：
応力とひずみの関数を使う2つ目の2D定常状態固体力学モデルを設定する：
解法

節点変位が与えられる．

基準の節点変位を指定する：
境界条件

構造は左側で固定されている．

構造を左側で固定する：

残りの面は自由に動く．

領域：
モデル領域を設定する：
テスト1
PDEモデルを解き，時間／メモリの使用量を監視する：
非アクティブなPDEをテストする：
テスト2
三角メッシュ上でPDEを解く：
非アクティブなPDEをテストする：
テスト3
PDEモデルを解き，時間／メモリの使用量を監視する：
非アクティブなPDEをテストする：
テスト4
PDEモデルを解き，時間／メモリの使用量を監視する：
非アクティブなPDEをテストする：
可視化

以下のセルはランタイムと消費メモリを節約するために評価不可にしてある．これらのセルを評価するためには，セルを選んでセル ▶ セルのプロパティを選び「評価可能」をチェックする．

変形した構造を可視化する：
垂直変位の解析解と数値解をプロットする：

SolidMechanics-FEM-Stationary-2D-PlaneStress-0005

モデル領域は合計の長さが ，高さが ，厚さが の梁である．梁は右境界で壁に固定されている．残りの境界は自由に動く．ヤング率は で与えられ，ポワソン比は である．これで梁理論に対応する．梁の中央(と固定されている端(の最大曲げ応力を求める．

テストの参照

S. H. Crandall, N. C. Dahl, An Introduction to the Mechanics of Solids, McGraw-Hill Book Co., Inc., New York, NY, 1959, pg. 342, problem 7.18.

方程式

厚さを指定した標準的な応力モデルを使う．

モデルの変数とパラメータを定義する：
2D定常状態固体力学モデルを設定する：
解法

中央と固定された端の最大曲げ応力を求める．

基準値を指定する：
境界条件

梁は右側で固定される．

右側で構造を固定し，荷重を適用する：
領域
モデル領域を設定する：
メッシュを可視化する：
解く
PDEモデルを解き，時間／メモリの使用量を監視する：
PDEモデルを解き，時間／メモリの使用量を監視する：
テスト1
最初の解をテストする：
テスト2
2つ目の解をテストする：
テスト3
3つ目の解をテストする：
テスト4
4つ目の解をテストする：
可視化

以下のセルはランタイムと消費メモリを節約するために評価不可にしてある．これらのセルを評価するためには，セルを選んでセル ▶ セルのプロパティを選び「評価可能」をチェックする．

変形した構造を可視化する：

SolidMechanics-FEM-Stationary-2D-PlaneStress-0006

モデル領域は合計の長さが ，高さが ，厚さが の梁である．梁は左境界で壁に固定される．右側では曲げモーメントと押上げ力の2つの荷重テストを行う．残りの境界は自由に動く．ヤング率は で与えられ，ポワソン比は である．それぞれのテストにおいて，自由端にはたわみがあり，左端から少し離れたところの曲げ応力が求められる．

テストの参照

R. J. Roark, Formulas for Stress and Strain, 4th Edition, McGraw-Hill Book Co., Inc., New York, NY, 1965, pp. 104, 106.

方程式

標準的な応力モデルを使う．

モデルの変数とパラメータを定義する：
2D定常状態固体力学モデルを設定する：
解法

基準値を与える：

基準値を指定する：
境界条件

梁は左側で固定される．

構造を左側で固定する：
領域
モデル領域を設定する：
メッシュを可視化する：
解く
PDEモデルを解き，時間／メモリの使用量を監視する：
PDEモデルを解き，時間／メモリの使用量を監視する：
テスト1
最初の解をテストする：
テスト2
2つ目の解をテストする：
テスト3
最初の変位をテストする：
テスト4
2つ目の変位をテストする：
テスト5
最初の変位をテストする：
可視化

以下のセルはランタイムと消費メモリを節約するために評価不可にしてある．これらのセルを評価するためには，セルを選んでセル ▶ セルのプロパティを選び「評価可能」をチェックする．

変形した構造を可視化する：

SolidMechanics-FEM-Stationary-2D-PlaneStress-0007

長方形板が底で固定されている．垂直ひずみがなくなり，せん断ひずみが一定であるように，左，上，右に3つの境界荷重が適用される．

61.gif

テストの参照

G. Backstrom, Simple displacement and Vibration, GB Publishing, 2006, ISBN: 9-1975553-20, Page 56

方程式

標準的な平面応力モデルを使う．

モデルの変数とパラメータを定義する：
2D定常状態固体力学モデルを設定する：
解法

基準値を与える：

基準値を指定する：
境界条件

板は底で固定され，圧力や力は残りの境界に作用する．

構造を底で固定する：
圧力をかける：
構造を底で固定し，力をかける：
領域
モデル領域を設定する：
解く
PDEモデルを解く：
テスト1
最初の解をテストする：
テスト2
2つ目の解をテストする：
テスト3
3つ目の解をテストする：
テスト4
4つ目の解をテストする：
可視化

以下のセルはランタイムと消費メモリを節約するために評価不可にしてある．これらのセルを評価するためには，セルを選んでセル ▶ セルのプロパティを選び「評価可能」をチェックする．

変形した構造を可視化する：

SolidMechanics-FEM-Stationary-2D-PlaneStrain-0001

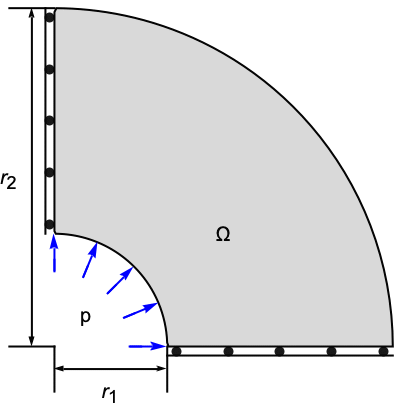
次のテストは2D平面ひずみ解析のさまざまな面を検証する．モデル領域は，内半径 ，外半径 ，厚さ のパイプの4分の1断面である．左境界にはパイプが上下に動ける対称制約，右下にはパイプが左右に動ける2つ目の対称制約がある．パイプ内部には圧力 が作用する．残りの境界は自由に動く．ヤング率は で与えられ，ポワソン比は である．

69.gif

テストの参照

M. Asghar Bhatti. Fundamental Finite Element Analysis and Applications. Wiley., Page 517, Example 7.9, Pressure Vessels

方程式

標準的な平面ひずみモデルを使う．

モデルの変数とパラメータを定義する：
2D定常状態固体力学モデルを設定する：
応力とひずみの関数を使う，2つ目の2D定常状態固体力学モデルを設定する：
解法

接線応力と半径応力を与える．

解析基準解を指定する：
境界条件

4分の1のパイプ構造は左側でy方向に対称条件を使う．

左側のy方向の対称条件：
底のx方向の対称条件：

内部には外向きの20単位の圧力がある．

内側で外向きに作用する境界荷重を設定する：

残りの辺は自由に動く．

領域
モデル領域を設定する：
テスト1
PDEを解き，ひずみと応力を計算する：
接線応力を検証する：
テスト2
接線応力を検証する：
テスト3
PDEを解き，ひずみと応力を計算する：
接線応力を検証する：
テスト4
接線応力を検証する：
可視化

以下のセルはランタイムと消費メモリを節約するために評価不可にしてある．これらのセルを評価するためには，セルを選んでセル ▶ セルのプロパティを選び「評価可能」をチェックする．

変形した構造を可視化する：

3D方程式

このセクションには，3D定常固体力学PDEモデルの例が含まれている．

SolidMechanics-FEM-Stationary-3D-0001

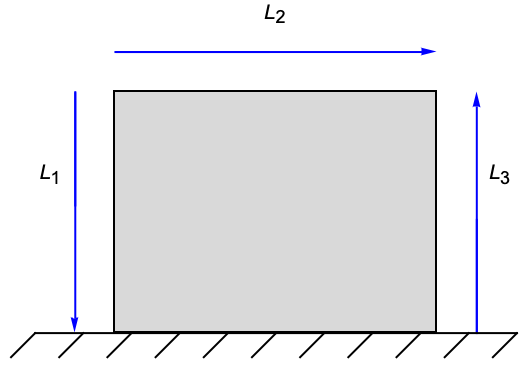
次のテストは3D応力解析を検証する．モデル領域は長さ，幅，高さの梁である．梁は左側で壁に固定されている．右側では の力が 方向に作用している．残りの境界は自由に動く．材料としてS235鋼を使う．ヤング率は で与えられ，ポワソン比は である．

78.gif

テストの参照

M. Brand, Grundlagen FEM mit Solidworks, Vieweg+Teuber, 2011, ISBN: 978-3-8348-1306-0, Page 7

方程式

標準的な応力モデルを使う．

モデルの変数とパラメータを定義する：
3D定常状態固体力学モデルを設定する：
応力とひずみの関数を使う，2つ目の3D定常状態固体力学モデルを設定する：
解法

方向で想定される伸張を与える．領域内部には応力を与える．伸張は以下で計算できる．

これは次に従っている．

の応力は計算すると以下になる．

基準値を指定する：
境界条件

構造は左側で固定される．

構造を左側で固定する：

右側には 方向に作用するの力がある．

右境界で 方向に作用する力を設定する．

残りの辺は自由に動く．

領域
六面体要素および四面体要素でモデル領域とメッシュを設定する：
メッシュを可視化する：
PDEモデルを解き，時間／メモリの使用量を監視する：
応力とひずみを計算する．
PDEモデルを解き，時間／メモリの使用量を監視する：
応力とひずみを計算する．
PDEモデルを解き，時間／メモリの使用量を監視する：
応力とひずみを計算する．
PDEモデルを解き，時間／メモリの使用量を監視する：
応力とひずみを計算する．
テスト1
最初のメッシュで最初のPDEをテストする：
テスト2
最初のメッシュで2つ目のPDEをテストする：
テスト3
2つ目のメッシュで最初のPDEをテストする：
テスト4
2つ目のメッシュで2つ目のPDEをテストする：
テスト5
最初のメッシュの最初の解の応力成分を検証する：
テスト6
最初のメッシュの2つ目の解の応力成分を検証する：
テスト7
2つ目のメッシュの最初の解の応力成分を検証する：
テスト8
2つ目のメッシュの2つ目の解の応力成分を検証する：
テスト9
最初のメッシュの最初の解のミーゼス応力成分を検証する：
テスト10
最初のメッシュの2つ目の解のミーゼス応力成分を検証する：
テスト11
2つ目のメッシュの最初の解のミーゼス応力成分を検証する：
テスト12
2つ目のメッシュの2つ目の解のミーゼス応力成分を検証する：
可視化

以下のセルはランタイムと消費メモリを節約するために評価不可にしてある．これらのセルを評価するためには，セルを選んでセル ▶ セルのプロパティを選び「評価可能」をチェックする．

変形した構造を可視化する：

SolidMechanics-FEM-Stationary-3D-0002

次のテストは3D応力解析を検証する．モデル領域は長さ，幅，高さの穴の開いた板である．穴は中央にあり，直径はである．板は左境界で壁に固定されている．右側では の力が 方向に作用している．残りの境界は自由に動く．材料としてS235鋼が使われる．ヤング率は で与えられ，ポワソン比は である．

106.gif

テストの参照

M. Brand, Grundlagen FEM mit Solidworks, Vieweg+Teuber, 2011, ISBN: 978-3-8348-1306-0, Page 13

方程式

標準的な応力モデルを使う．

モデルの変数とパラメータを定義する：
3D定常状態固体力学モデルを設定する：
応力とひずみの関数を使う2つ目の3D定常状態固体力学モデルを設定する：
解法

想定されるミーゼス応力の最大値を与える．

ミーゼス応力の解析推定は以下で与えられる．

ここで はルックアップテーブルからの応力集中係数である．この場合，穴の半径と板の高さの半分の縦横比は以下になる．

穴を通した断面への公称応力 は計算すると以下になる．

したがって想定される最大応力は次のようになる．

基準値を指定する：
境界条件

構造は左側で固定される．

構造を左側で固定する：

右側には， 方向に作用するの力がある．

右に作用する境界荷重を設定する：

残りの面は自由に動く．

領域
六面体要素および四面体要素でモデル領域とメッシュを設定する：
メッシュを可視化する：
PDEモデルを解き，時間／メモリの使用量を監視する：
ひずみ，応力，ミーゼス応力を計算する：
PDEモデルを解き，時間／メモリの使用量を監視する：
ひずみ，応力，ミーゼス応力を計算する：
テスト1
最初のメッシュの最初のPDEをテストする：
テスト2
最初のメッシュの2つ目のPDEをテストする：
可視化

以下のセルはランタイムと消費メモリを節約するために評価不可にしてある．これらのセルを評価するためには，セルを選んでセル ▶ セルのプロパティを選び「評価可能」をチェックする．

ミーゼス応力を可視化する：

SolidMechanics-FEM-Stationary-3D-0003

次のテストは，適用された境界荷重を検証する．モデル領域は長さ，幅，高さの梁である．梁は左境界で壁に固定されている．右側では の力が負の 方向に作用している．残りの境界は自由に動く．材料としてS275鋼を使う．ヤング率は で与えられ，ポワソン比は である．

127.gif

テストの参照

M. Brand, Grundlagen FEM mit Solidworks, Vieweg+Teuber, 2011, ISBN: 978-3-8348-1306-0, Page 29

方程式

標準的な応力モデルを使う．

モデルの変数とパラメータを定義する：
3D定常状態固体力学モデルを設定する：
応力とひずみの関数を使う2つ目の3D定常状態固体力学モデルを設定する：
解法

負のz方向で想定される最大変位を与える．

z方向の最大たわみの解析推定は以下で与えられる．

ここで運動は である． は適用された力， は梁の長さである．

基準値を指定する：
境界条件

構造は左側で固定される．

構造を左側で固定する：

右側には，負の 方向にの力が作用している．

右に下向きに作用する境界荷重を設定する：

残りの面は自由に動く．

領域
六面体要素および四面体要素でモデル領域とメッシュを設定する：
メッシュを可視化する：
PDEモデルを解き，時間／メモリの使用量を監視する：
PDEモデルを解き，時間／メモリの使用量を監視する：
PDEモデルを解き，時間／メモリの使用量を監視する：
PDEモデルを解き，時間／メモリの使用量を監視する：
テスト1
最初のメッシュの最初のPDEをテストする：
テスト2
最初のメッシュの2つ目のPDEをテストする：
テスト3
2つ目のメッシュの最初のPDEをテストする：
テスト4
2つ目のメッシュの2つ目のPDEをテストする：
コメント

この例はされに進んで梁と壁の固定点における垂直応力を計算する．応力特異性があるため，数値は解析解から逸れる．与えられた参照では，解析応力値と特異点近くで数値的に計算された値を比較するために任意の点が選ばれている．これは最適なアプローチとは思えないのでこのテストは飛ばすことにする．

SolidMechanics-FEM-Stationary-3D-0004

以下のテストは分布荷重を検証する．モデル領域は長さ，幅，高さの梁である．梁は左境界で壁に固定されている．上面ではの荷重が適用され負の 方向に作用している．長さあたりの力の単位に注意する．残りの境界は自由に動く．材料としてS275鋼を使う．ヤング率は で与えられ，ポワソン比は である．

147.gif

テストの参照

M. Brand, Grundlagen FEM mit Solidworks, Vieweg+Teuber, 2011, ISBN: 978-3-8348-1306-0, Page 32

方程式

標準的な応力モデルを使う．材料パラメータはミリメートルの単位で与えられる．

モデルの変数とパラメータを定義する：
3D定常状態固体力学モデルを設定する：
応力とひずみの関数を使う2つ目の3D定常状態固体力学モデルを設定する：
解法

負のz方向に想定される最大変位を与える．

方向の最大たわみの解析推定は以下で与えられる．

ここで運動は である． は適用される分布力， は梁の長さである．

基準値を指定する：
境界条件

構造は左側で固定される．

構造を左側で固定する：

上部ではの分布力が負の 方向に作用している．梁の長さはなので，作用している合計の力はである．

上部に作用する境界荷重を設定する：

残りの面は自由に動く．

領域
六面体要素および四面体要素でモデル領域とメッシュを設定する：
メッシュを可視化する：
PDEモデルを解き，時間／メモリの使用量を監視する：
PDEモデルを解き，時間／メモリの使用量を監視する：
PDEモデルを解き，時間／メモリの使用量を監視する：
PDEモデルを解き，時間／メモリの使用量を監視する：
テスト1
最初のメッシュの最初のPDEをテストする：
テスト2
最初のメッシュの2つ目のPDEをテストする：
テスト3
2つ目のメッシュの最初のPDEをテストする：
テスト4
2つ目のメッシュの2つ目のPDEをテストする：
コメント

この例はされに進んで梁と壁の固定点における垂直応力を計算する．応力特異性があるため，数値は解析解から逸れる．与えられた参照では，解析応力値と特異点近くで数値的に計算された値を比較するために任意の点が選ばれている．これは最適なアプローチとは思えないのでこのテストは飛ばすことにする．

SolidMechanics-FEM-Stationary-3D-0005

次のテストはトルクの境界荷重を検証する．モデル領域は，長さ，直径の棒である．棒は左境界で壁に固定されている．右端にはのモーメントが適用される．残りの境界は自由に動く．材料としてS275鋼を使う．ヤング率は で与えられ，ポワソン比は である．

169.gif

テストの参照

M. Brand, Grundlagen FEM mit Solidworks, Vieweg+Teuber, 2011, ISBN: 978-3-8348-1306-0, Page 35

方程式

標準的な応力モデルを使う．

モデルの変数とパラメータを定義する：
3D定常状態固体力学モデルを設定する：
応力とひずみの関数を使う2つ目の3D定常状態固体力学モデルを設定する：
解法
基準値を指定する：
境界条件

構造は左端で固定されている．

構造を左端で固定する：

右端にはのトルクがかかる．このトルク は表面圧力に変換しなければならない．以下から始める．

ここで はせん断応力（圧力）， は半径，は断面二次モーメント[m^4]である．配置し直すと次のようになる．

右側に作用する境界荷重を設定する：

残りの面は自由に動く．

領域
モデル領域を設定して粗いメッシュを作成する：
メッシュを可視化する：
PDEモデルを解き，時間／メモリの使用量を監視する：
PDEモデルを解き，時間／メモリの使用量を監視する：
テスト1
最初のPDEをテストする：
テスト2
2つ目のPDEをテストする：
テスト3
最大ミーゼス応力を検証する．
テスト4
2つ目のメッシュで2つ目のPDEをテストする：

SolidMechanics-FEM-Stationary-3D-0006

断面が矩形で長さが の先細のアルミ合金棒が底で固定されている．棒の自由端には軸荷重 が適用される．

テストの参照

C. O. Harris, Introduction to Stress Analysis, The Macmillan Co., New York, NY, 1959, pg. 237, problem 4.

方程式

標準的な応力モデルを使う．

モデルの変数とパラメータを定義する：
3D定常状態固体力学モデルを設定する：
応力とひずみの関数を使う2つ目の3D定常状態固体力学モデルを設定する：
基準値を指定する：
境界条件

棒は底で固定されている．

棒を底(z = 0)で固定し，力を加える：
領域
モデル領域を設定する：
メッシュを可視化する：
解く
最初のPDEモデルを解き，時間／メモリ使用量を監視する：
2つ目のPDEモデルを解き，時間／メモリ使用量を監視する：
テスト1
最初の解をテストする：
テスト2
2つ目の解をテストする：
テスト3
2つ目のPDEの最初の解をテストする：
テスト4
2つ目のPDEの2つ目の解をテストする：

固有モード解析

2D方程式

このセクションには2D固有モード固体力学PDE解析の例が含まれている．

SolidMechanics-FEM-Stationary-2D-Eigenmode-0001

次のテストは梁の2D平面応力解析を検証する．モデル領域は合計の長さが ，高さが ，厚さが の梁である．梁は左境界で壁に固定されている．残りの境界は自由に動く．ヤング率は で与えられ，ポワソン比は である．質量密度はで与えられる．

190.gif

テストの参照

なし

方程式

標準的な応力モデルを使う．

モデルの変数とパラメータを定義する：
2D定常状態固体力学モデルを設定する：
解法

想定される固有周波数 は以下で計算する：

ここで はヤング率， は高さ， は幅， は質量密度， は梁の長さであり，は以下になる：

よって次のようになる．

基準値を指定する：
境界条件

梁は左端で固定されている．

構造を左側で固定する：
領域
モデル領域を設定する：
メッシュを可視化する：
解く
PDEモデルを解き，時間／メモリの使用量を監視する：
PDEモデルを解き，時間／メモリの使用量を監視する：
テスト1
最初の解をテストする：
テスト2
2つ目の解をテストする：
可視化

以下のセルはランタイムと消費メモリを節約するために評価不可にしてある．これらのセルを評価するためには，セルを選んでセル ▶ セルのプロパティを選び「評価可能」をチェックする．

変形した構造を可視化する：

3D方程式

このセクションには3D固有モード固体力学PDE解析の例が含まれている．

SolidMechanics-FEM-Eigenmode-3D-0001

次のテストは3D固有モード解析を検証する．モデル領域は長さ，幅，高さの梁である．梁は左境界で壁に固定されている．残りの境界は自由に動く．ヤング率は で与えられ，ポワソン比は である．質量密度は である．

210.gif

テストの参照

なし

方程式

標準的な応力モデルを使う．

モデルの変数とパラメータを定義する：
3D定常状態固体力学モデルを設定する：
解法

想定される固有周波数 は次で計算する：

ここで はヤング率， は慣性モーメント， は質量密度， は断面積， は梁の長さである． は振動形式に依存する因数であり で与えられる．

したがって以下のようになる．

基準値を指定する：
境界条件

この構造は左側で固定されている．

構造を左側で固定する：

残りの面は自由に動く．

領域
六面体要素および四面体要素でモデル領域とメッシュを設定する：
メッシュを可視化する：
PDEモデルを解き，時間／メモリの使用量を監視する：
PDEモデルを解き，時間／メモリの使用量を監視する：
テスト1
最初の解をテストする：
テスト2
2つ目の解をテストする：
可視化

以下のセルはランタイムと消費メモリを節約するために評価不可にしてある．これらのセルを評価するためには，セルを選んでセル ▶ セルのプロパティを選び「評価可能」をチェックする．

変形した構造を可視化する：

SolidMechanics-FEM-Eigenmode-3D-0002

次のテストは3D固有モード解析を検証する．モデル領域は高さ，内半径，外半径 の円筒である．円筒は自由に動く．ヤング率は で与えられ，ポワソン比は である．質量密度は である．

230.gif

テストの参照

F. Abassian, D.J. Dawswell, and N.C. Knowles, Free Vibration Benchmarks, vol.3, NAFEMS, Glasgow, 1987.

方程式

標準的な応力モデルを使う．

モデルの変数とパラメータを定義する：
固有モード解析のための3D定常状態固体力学モデルを設定する：
固有モード解析のためではない2つ目の3D定常状態固体力学モデルを設定する：
解法

想定される固有周波数 は次で計算できる：

ここで は質量密度， は円筒の高さ， は剛性率である：

ここで はヤング率， はポアソン比である．

したがって以下のようになる：

基準値を指定する：
境界条件

円筒には制約条件がなく，自由に動く．

領域
四面体要素および角柱要素でモデル領域とメッシュを設定する：
FEMAddOnsパクレットをダウンロードして，六面体要素のメッシュを設定する．
メッシュを可視化する：

次にさまざまなメッシュ上でいろいろなPDEモデルを解く．

PDEモデルを解き，時間／メモリの使用量を監視する：
PDEモデルを解き，時間／メモリの使用量を監視する：
PDEモデルを解き，時間／メモリの使用量を監視する：
PDEモデルを解き，時間／メモリの使用量を監視する：
PDEモデルを解き，時間／メモリの使用量を監視する：
PDEモデルを解き，時間／メモリの使用量を監視する：
テスト1
最初のメッシュで最初の解をテストする：
テスト2
最初のメッシュで2つ目の解をテストする：
テスト3
最初のメッシュ（固有モード）で最初の解をテストする：
テスト4
最初のメッシュ（固有モード）で2つ目の解をテストする：
テスト5
2つ目のメッシュで最初の解をテストする：
テスト6
2つ目のメッシュで2つ目の解をテストする：
テスト7
2つ目のメッシュ（固有モード）で最初の解をテストする：
テスト8
2つ目のメッシュ（固有モード）で2つ目の解をテストする：
テスト9
3つ目のメッシュで最初の解をテストする：
テスト10
3つ目のメッシュで2つ目の解をテストする：
テスト11
3つ目のメッシュ（固有モード）で最初の解をテストする：
テスト12
3つ目のメッシュ（固有モード）で2つ目の解をテストする：
可視化

以下のセルはランタイムと消費メモリを節約するために評価不可にしてある．これらのセルを評価するためには，セルを選んでセル ▶ セルのプロパティを選び「評価可能」をチェックする．

変形した構造を可視化する：

テスト結果の検査

このセクションには，テストランの評価が含まれている．このためにTestResultObjectのすべてを収集し，TestReportを生成する．

ノートブックからTestResultObjectを抽出し，TestReportを生成する：
失敗したテストランを調べる．

結果の表が空ならば，すべてのテストは成功したということである．