AccuracyGoal

✖
`AccuracyGoal`

✖

is an option for various numerical operations which specifies how many effective digits of accuracy should be sought in the final result.

Details

AccuracyGoal is an option for such functions as NIntegrate, NDSolve, and FindRoot.
AccuracyGoal->Automatic normally yields an accuracy goal equal to half the setting for WorkingPrecision.
AccuracyGoal->Infinity specifies that accuracy should not be used as the criterion for terminating the numerical procedure. PrecisionGoal is typically used in this case.
Even though you may specify AccuracyGoal->n, the results you get may sometimes have much less than n‐digit accuracy.
In most cases, you must set WorkingPrecision to be at least as large as AccuracyGoal.
AccuracyGoal effectively specifies the absolute error allowed in a numerical procedure.
With AccuracyGoal->a and PrecisionGoal->p, the Wolfram Language attempts to make the numerical error in a result of size 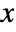be less than .

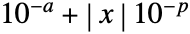Examples

open allclose all

Basic Examples (2)Summary of the most common use cases

Approximate a numerical integral to at least 8 digits of accuracy:

In[1]:=1

✖

https://wolfram.com/xid/09byxyt36-gn6dr6

Out[1]=1

Use precision (relative error) as the basis for error control in solving an ODE:

In[1]:=1

✖

https://wolfram.com/xid/09byxyt36-cm9ras

Out[1]=1

The relative error is small:

In[2]:=2

✖

https://wolfram.com/xid/09byxyt36-bz7zbd

In[3]:=3

✖

https://wolfram.com/xid/09byxyt36-m7d68x

Out[3]=3

Without specifying the AccuracyGoal, the relative error is much larger:

In[4]:=4

✖

https://wolfram.com/xid/09byxyt36-bgbxwg

Out[4]=4

Scope (2)Survey of the scope of standard use cases

Find a minimum with convergence criteria and :

In[1]:=1

✖

https://wolfram.com/xid/09byxyt36-4me3t

In[2]:=2

✖

https://wolfram.com/xid/09byxyt36-05x0hq

Out[2]=2

Use convergence criteria and :

In[3]:=3

✖

https://wolfram.com/xid/09byxyt36-hr5egj

Out[3]=3

Use convergence criteria and not possible at machine precision:

In[4]:=4

✖

https://wolfram.com/xid/09byxyt36-cr7e7f

Out[4]=4

Use a higher working precision to allow convergence:

In[5]:=5

✖

https://wolfram.com/xid/09byxyt36-vxc4p

Out[5]=5

Solve a differential equation using high-precision arithmetic:

In[1]:=1

✖

https://wolfram.com/xid/09byxyt36-kp2vn2

Out[1]=1

In[2]:=2

✖

https://wolfram.com/xid/09byxyt36-jlz4gu

Out[2]=2

Use AccuracyGoal and PrecisionGoal at half the 32-digit working precision:

In[3]:=3

✖

https://wolfram.com/xid/09byxyt36-fu2mbl

Out[3]=3

This corresponds to the automatic setting used by NDSolve:

In[4]:=4

✖

https://wolfram.com/xid/09byxyt36-ipsbla

Out[4]=4

Top