AcyclicGraphQ

AcyclicGraphQ[g]

グラフ g が非巡回グラフの場合はTrueを，そうでなければFalseを返す．

詳細

  • ある頂点から始まり同じ頂点で終る経路があるグラフは巡回グラフである．

予備知識

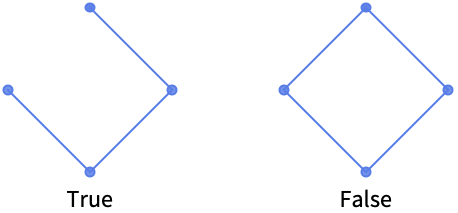
  • AcyclicGraphQは，グラフに閉路があるかどうかをチェックする．グラフの閉路（閉路が特定の端点がある明示的な経路を使って設定された場合は回路と呼ぶ方がふさわしい）は，経路の最初のノードが最後のノードと一致するような，連結経路を形成するグラフの辺集合の部分集合である．閉路のないグラフは非巡回グラフと呼ばれるのに対し，1つあるいはそれ以上の閉路を含むグラフは巡回グラフと呼ばれる．AcyclicGraphQは非巡回グラフに対してTrueを返し（自己ループは無視される），その他の場合はFalseを返す．
  • 長さ3の閉路を含まない単純グラフはTriangle-Freeグラフと呼ばれ，長さ4の閉路を含まない単純グラフはSquare-Freeグラフと呼ばれる．このため，非巡回単純グラフは，Triangle-FreeかつSquare-Freeである．また，非ハミルトングラフでもある（つまり，ハミルトン閉路を含まない）．
  • 非巡回連結グラフはツリーとして知られている．このため，すべてのツリーは定義上非巡回グラフであり，TreeGraphQ（AcyclicGraphQとConnectedGraphQの論理結合に等しい）を使ってグラフがツリーかどうかを調べることができる．ツリーはコンピュータサイエンスの分野で，特にディスク上のファイルとフォルダのストレッジを含むアルゴリズムとデータ構造の実装に，広く使われている．
  • 必ずしも連結されていない非巡回グラフはフォレストとして知られている．有向辺のあるフォレストは，非巡回有向グラフ(DAG)として，よりよく知られているかもしれない．DAGは，したがって，AcyclicGraphQとDirectedGraphQの両方がTrueを返すグラフである．DAGは，電子回路，情報のフロー，エベントとタスクのような，多くの種類の情報のモデル化に重要である．
  • FindCycleを使って，非巡回グラフではないグラフ中の1つあるいは複数の閉路を求めることができる（グラフが非巡回グラフの場合は，空リスト{} が返される）．

例題

すべて開くすべて閉じる

例  (2)

グラフが非巡回グラフかどうか調べる：

すべてのグラフが非巡回グラフであるわけではない：

スコープ  (6)

AcyclicGraphQは無向グラフに使うことができる：

有向グラフに使う：

多重グラフに使う：

混合グラフに使う：

グラフ以外のものに対してはAcyclicGraphQはFalseを返す：

AcyclicGraphQは大きいグラフに使うことができる：

アプリケーション  (1)

凝縮グラフは非巡回である：

凝縮グラフの頂点は強連結成分である：

凝縮グラフを構築する：

このグラフが非巡回であることを証明する：

特性と関係  (6)

DepthFirstScanを使ってグラフの中の回路を求める：

AcyclicGraphQと比較する：

CycleGraphは非巡回グラフではない：

TreeGraphは非巡回グラフである：

始点と終点の頂点が異なるPathGraphは非巡回グラフである：

非巡回グラフはハミルトングラフではない：

最小頂点次数が2より大きいグラフは非巡回グラフではない：

考えられる問題  (1)

AcyclicGraphQは自己ループを無視する：

Wolfram Research (2010), AcyclicGraphQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/AcyclicGraphQ.html.

テキスト

Wolfram Research (2010), AcyclicGraphQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/AcyclicGraphQ.html.

CMS

Wolfram Language. 2010. "AcyclicGraphQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AcyclicGraphQ.html.

APA

Wolfram Language. (2010). AcyclicGraphQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AcyclicGraphQ.html

BibTeX

@misc{reference.wolfram_2024_acyclicgraphq, author="Wolfram Research", title="{AcyclicGraphQ}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/AcyclicGraphQ.html}", note=[Accessed: 15-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_acyclicgraphq, organization={Wolfram Research}, title={AcyclicGraphQ}, year={2010}, url={https://reference.wolfram.com/language/ref/AcyclicGraphQ.html}, note=[Accessed: 15-November-2024 ]}