WOLFRAM

Wolfram Language & System Documentation Center

TreeGraphQ[g]

yields True if the graph g is a tree and False otherwise.

Details
Details and Options Details and Options
Examples  
Basic Examples  
Scope  
Properties & Relations  
Possible Issues  
See Also
Related Guides
History
Cite this Page

TreeGraphQ

TreeGraphQ[g]

yields True if the graph g is a tree and False otherwise.

Details

  • A tree is a simple connected graph with no cycles.

Examples

open all close all

Basic Examples  (2)

Test whether a graph is a tree:

A graph with cycles is not a tree:

Scope  (6)

TreeGraphQ works with undirected graphs:

Directed graphs:

Multigraphs:

Mixed graphs:

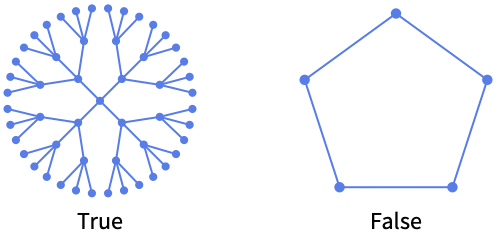
TreeGraphQ gives False for anything that is not a tree graph:

TreeGraphQ works with large graphs:

Properties & Relations  (10)

A tree graph can be a simple graph:

A tree graph can be a weighted graph:

A star is a special tree with as many leaves as possible:

A path graph with no repeated vertices is a tree with two leaves:

A graph with self-loops is not a tree graph:

A graph with cycles is not a tree graph:

A disconnected graph is not a tree graph:

A tree graph with vertices has edges:

A tree graph is a bipartite graph:

A tree graph is not Hamiltonian:

Possible Issues  (1)

TreeGraphQ gives False for non-explicit graphs:

Wolfram Research (2010), TreeGraphQ, Wolfram Language function, https://reference.wolfram.com/language/ref/TreeGraphQ.html.

Text

Wolfram Research (2010), TreeGraphQ, Wolfram Language function, https://reference.wolfram.com/language/ref/TreeGraphQ.html.

CMS

Wolfram Language. 2010. "TreeGraphQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TreeGraphQ.html.

APA

Wolfram Language. (2010). TreeGraphQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TreeGraphQ.html

BibTeX

@misc{reference.wolfram_2025_treegraphq, author="Wolfram Research", title="{TreeGraphQ}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/TreeGraphQ.html}", note=[Accessed: 05-August-2025]}

BibLaTeX

@online{reference.wolfram_2025_treegraphq, organization={Wolfram Research}, title={TreeGraphQ}, year={2010}, url={https://reference.wolfram.com/language/ref/TreeGraphQ.html}, note=[Accessed: 05-August-2025]}