AcyclicGraphQ
背景
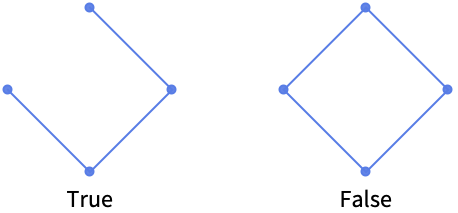
- AcyclicGraphQ 检查图是否无圈. 图的圈(若该圈被显式路径标明且路径由特定端点组成,则更适合被称为环路)是该图边集合的子集,且构成起点终点相同的连通路径. 没有圈的图被称为无圈图,含有一个或多个圈的图则被称为有圈图. 对有圈图(忽略自环),AcyclicGraphQ 给出 True 否则给出 False .
- 不含有长度为三的圈的简单图被称为无三角图,而不含有长度为四的圈的简单图被称为无方形图. 因此简单无圈图是无三角且无方形的,也是非哈密尔顿的(即不含有哈密尔顿圈).
- 连通无圈图被称为树. 因此根据定义所有的树都是无圈的,而 TreeGraphQ(等价于 AcyclicGraphQ 和 ConnectedGraphQ 的逻辑合取) 可用于检查一个图是否是树. 树在计算机科学和许多算法及数据结构的实现中大量出现,比如存储在磁盘上的文件与文件夹.
- 未必连通的无圈图被称为森林. 带有向边的森林通常被称为有向无圈图或 DAG. 因此 DAG 是 AcyclicGraphQ 和 DirectedGraphQ 都会给出 True 的图. DAG 在各种信息的建模中很重要,比如电子电路、信息流、事件和任务等.
- FindCycle 可用于从非无圈图中找出一个或多个圈(对无圈图则返回空集 {}).
范例
打开所有单元关闭所有单元范围 (6)
属性和关系 (6)
使用 DepthFirstScan 来检测图中的圈:
与 AcyclicGraphQ 比较:
CycleGraph 不是无圈图:
TreeGraph 是无圈图:
具有不同初始和终止顶点的 PathGraph 是无圈图:
可能存在的问题 (1)
AcyclicGraphQ 忽略自环:
Wolfram Research (2010),AcyclicGraphQ,Wolfram 语言函数,https://reference.wolfram.com/language/ref/AcyclicGraphQ.html.
文本
Wolfram Research (2010),AcyclicGraphQ,Wolfram 语言函数,https://reference.wolfram.com/language/ref/AcyclicGraphQ.html.
CMS
Wolfram 语言. 2010. "AcyclicGraphQ." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/AcyclicGraphQ.html.
APA
Wolfram 语言. (2010). AcyclicGraphQ. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/AcyclicGraphQ.html 年