BilateralHypergeometricPFQ[{a1,…,ap},{b1,…,bq},z]
両側超幾何関数 ![]() である.
である.




BilateralHypergeometricPFQ
BilateralHypergeometricPFQ[{a1,…,ap},{b1,…,bq},z]
両側超幾何関数 ![]() である.
である.
詳細

- 両側超幾何級数は項について一般化された超幾何級数と同じような定義を持つが,すべての整数を合計すると二重無限級数が形成される.
- 記号操作・数値操作の両方に適した数学関数である.
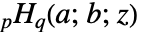 は級数展開
は級数展開 ![sum_(k=-infty)^(infty)TemplateBox[{{a, _, 1}, k}, Pochhammer]...TemplateBox[{{a, _, p}, k}, Pochhammer]/TemplateBox[{{b, _, 1}, k}, Pochhammer]...TemplateBox[{{b, _, q}, k}, Pochhammer]z^k sum_(k=-infty)^(infty)TemplateBox[{{a, _, 1}, k}, Pochhammer]...TemplateBox[{{a, _, p}, k}, Pochhammer]/TemplateBox[{{b, _, 1}, k}, Pochhammer]...TemplateBox[{{b, _, q}, k}, Pochhammer]z^k](Files/BilateralHypergeometricPFQ.ja/3.png) を持つ.ただし,
を持つ.ただし,![TemplateBox[{a, k}, Pochhammer] TemplateBox[{a, k}, Pochhammer]](Files/BilateralHypergeometricPFQ.ja/4.png) はPochhammer記号である.
はPochhammer記号である.- 両側超幾何級数
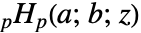 は,
は, 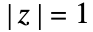 で
で 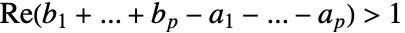 であれば収束する.
であれば収束する. 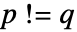 のとき,両側超幾何級数
のとき,両側超幾何級数 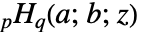 はBorel正則化を使って計算される.
はBorel正則化を使って計算される.- パラメータ
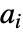 はどれも正の整数であってはならず,
はどれも正の整数であってはならず,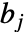 はどれも負の整数であってはならない.
はどれも負の整数であってはならない. - BilateralHypergeometricPFQは任意の数値精度で評価できる.
- 特別な引数の場合,BilateralHypergeometricPFQは自動的に厳密値を計算する.
- BilateralHypergeometricPFQは自動的にリストに縫い込まれる.
例題
すべて開く すべて閉じるスコープ (18)
数値評価 (4)
BilateralHypergeometricPFQを高精度で効率的に評価する:
BilateralHypergeometricPFQはその第3引数のリストに要素単位で縫い込まれる:
特定の値 (3)
特別なパラメータの場合,BilateralHypergeometricPFQを評価すると自動的により簡単な関数になる:
![]() におけるBilateralHypergeometricPFQ:
におけるBilateralHypergeometricPFQ:
![]() の際の
の際の![]() におけるBilateralHypergeometricPFQ:
におけるBilateralHypergeometricPFQ:
積分 (2)
微分 (1)
特定のBilateralHypergeometricPFQの一次導関数:
このBilateralHypergeometricPFQの ![]() 次導関数:
次導関数:
級数展開 (3)
原点におけるBilateralHypergeometricPFQの級数展開を計算する:
BilateralHypergeometricPFQのInfinityにおける級数展開を計算する:
BilateralHypergeometricPFQの生成点における級数展開を計算する:
アプリケーション (1)
BilateralHypergeometricPFQを介して二重無限和を計算する:
特性と関係 (2)
BilateralHypergeometricPFQは,2つのHypergeometricPFQの和として書けることがある:
BilateralHypergeometricPFQは初等関数に簡約されることがある:
考えられる問題 (1)
![]() のときBilateralHypergeometricPFQはBorel正則化を使うが,これには時間がかかるかもしれない:
のときBilateralHypergeometricPFQはBorel正則化を使うが,これには時間がかかるかもしれない:
おもしろい例題 (1)
BilateralHypergeometricPFQはより簡単な特殊関数に自動的に簡約されることがある:

テキスト
Wolfram Research (2024), BilateralHypergeometricPFQ, Wolfram言語関数, https://reference.wolfram.com/language/ref/BilateralHypergeometricPFQ.html.
CMS
Wolfram Language. 2024. "BilateralHypergeometricPFQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BilateralHypergeometricPFQ.html.
APA
Wolfram Language. (2024). BilateralHypergeometricPFQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BilateralHypergeometricPFQ.html
BibTeX
@misc{reference.wolfram_2025_bilateralhypergeometricpfq, author="Wolfram Research", title="{BilateralHypergeometricPFQ}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/BilateralHypergeometricPFQ.html}", note=[Accessed: 14-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_bilateralhypergeometricpfq, organization={Wolfram Research}, title={BilateralHypergeometricPFQ}, year={2024}, url={https://reference.wolfram.com/language/ref/BilateralHypergeometricPFQ.html}, note=[Accessed: 14-February-2026]}