BilateralHypergeometricPFQ
BilateralHypergeometricPFQ[{a1,…,ap},{b1,…,bq},z]
是双边超几何函数 ![]() .
.
更多信息

- 双边超几何级数的项与广义超几何级数具有类似的定义,但是它对所有整数求和,因此形成了一个双向无穷级数.
- 数学函数,适用于符号和数值操作.
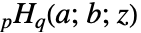 具有级数展开式
具有级数展开式 ![sum_(k=-infty)^(infty)TemplateBox[{{a, _, 1}, k}, Pochhammer]...TemplateBox[{{a, _, p}, k}, Pochhammer]/TemplateBox[{{b, _, 1}, k}, Pochhammer]...TemplateBox[{{b, _, q}, k}, Pochhammer]z^k sum_(k=-infty)^(infty)TemplateBox[{{a, _, 1}, k}, Pochhammer]...TemplateBox[{{a, _, p}, k}, Pochhammer]/TemplateBox[{{b, _, 1}, k}, Pochhammer]...TemplateBox[{{b, _, q}, k}, Pochhammer]z^k](Files/BilateralHypergeometricPFQ.zh/3.png) ,其中
,其中 ![TemplateBox[{a, k}, Pochhammer] TemplateBox[{a, k}, Pochhammer]](Files/BilateralHypergeometricPFQ.zh/4.png) 是 Pochhammer 符号.
是 Pochhammer 符号.- 如果
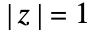 且
且 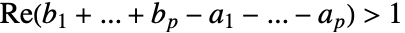 ,双边超几何级数
,双边超几何级数 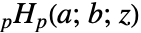 是收敛的.
是收敛的. - 当
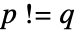 时,双边超几何函数
时,双边超几何函数 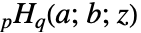 使用 Borel 正则化计算.
使用 Borel 正则化计算. - 参数
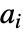 不能为正整数,
不能为正整数,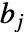 不能为负整数.
不能为负整数. - BilateralHypergeometricPFQ 可以计算为任意数值精度.
- 对于某些特殊参数,BilateralHypergeometricPFQ 自动计算出精确值.
- BilateralHypergeometricPFQ 自动在列表上进行线程操作.
范例
打开所有单元关闭所有单元范围 (18)
数值运算 (4)
高精度高效地运算 BilateralHypergeometricPFQ:
BilateralHypergeometricPFQ 在其第三个参数上逐元素线性作用于列表:
具体值 (3)
对于某些参数,BilateralHypergeometricPFQ 自动运算为较简单的函数:
BilateralHypergeometricPFQ 在 ![]() 处:
处:
对于 ![]() 的情况,BilateralHypergeometricPFQ 在
的情况,BilateralHypergeometricPFQ 在 ![]() 处:
处:
积分 (2)
求导 (1)
特定 BilateralHypergeometricPFQ 的一阶导数:
BilateralHypergeometricPFQ 的 ![]() 阶导数:
阶导数:
级数展开 (3)
计算 BilateralHypergeometricPFQ 在原点处的级数展开式:
计算 BilateralHypergeometricPFQ 在 Infinity 处的级数展开式:
计算 BilateralHypergeometricPFQ 在通点处的级数展开:
应用 (1)
通过 BilateralHypergeometricPFQ 计算双向无穷和:
属性和关系 (2)
可能存在的问题 (1)
当 ![]() 时,BilateralHypergeometricPFQ 使用 Borel 正则化,这可能很耗时:
时,BilateralHypergeometricPFQ 使用 Borel 正则化,这可能很耗时:
巧妙范例 (1)
BilateralHypergeometricPFQ 可以自动简化为更简单的特殊函数:
文本
Wolfram Research (2024),BilateralHypergeometricPFQ,Wolfram 语言函数,https://reference.wolfram.com/language/ref/BilateralHypergeometricPFQ.html.
CMS
Wolfram 语言. 2024. "BilateralHypergeometricPFQ." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/BilateralHypergeometricPFQ.html.
APA
Wolfram 语言. (2024). BilateralHypergeometricPFQ. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BilateralHypergeometricPFQ.html 年