BiquadraticFilterModel[{ω,q}]
creates a lowpass biquadratic filter using the characteristic frequency ω and the quality factor q.
BiquadraticFilterModel[{"type",spec}]
creates a filter of a given {"type",spec}.
BiquadraticFilterModel[{"type",spec},var]
expresses the model in terms of the variable var.


BiquadraticFilterModel
BiquadraticFilterModel[{ω,q}]
creates a lowpass biquadratic filter using the characteristic frequency ω and the quality factor q.
BiquadraticFilterModel[{"type",spec}]
creates a filter of a given {"type",spec}.
BiquadraticFilterModel[{"type",spec},var]
expresses the model in terms of the variable var.
Details

- Biquadratic filters are second-order filters defined by a ratio of two quadratic polynomials. They are among the most commonly used circuits in analog and digital signal processing.
- BiquadraticFilterModel returns the filter as a TransferFunctionModel.
- Filter specifications {"type",spec} can be any of the following:
-
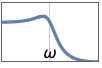
{"Lowpass",{{ω,q}}} uses cutoff frequency ω and quality factor q 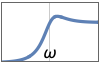
{"Highpass",{{ω,q}}} uses cutoff frequency ω and quality factor q 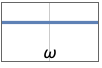
{"Allpass",{{ω,q}}} uses frequency ω and quality factor q 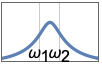
{"Bandpass",{ω1,ω2}} uses corner frequencies ω1 and ω2 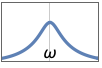
{"Bandpass",{{ω,q}}} uses center frequency ω and quality factor q 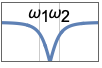
{"Bandstop",{ω1,ω2}} uses corner frequencies ω1 and ω2 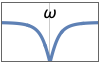
{"Bandstop",{{ω,q}}} uses center frequency ω and quality factor q - The following filter specifications can be given to create equalizers:
-
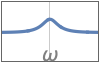
{"Peaking",{{ω,q}},g} peaking equalizer using gain value g 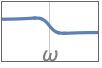
{"LowShelf",{{ω,q}},g} lowpass shelving equalizer using gain value g 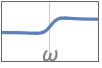
{"HighShelf",{{ω,q}},g} highpass shelving equalizer using gain value g - Given the gain value
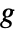 , the attenuation is
, the attenuation is 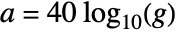 .
.
Examples
open all close allBasic Examples (3)
Scope (8)
A symbolic lowpass filter with cutoff frequency ω and quality factor ![]() :
:
A symbolic highpass filter with cutoff frequency ![]() and quality factor
and quality factor ![]() :
:
A symbolic bandpass filter with center frequency ![]() and quality factor
and quality factor ![]() :
:
A symbolic bandstop filter with center frequency ![]() and quality factor
and quality factor ![]() :
:
A symbolic allpass filter with center frequency ![]() and quality factor
and quality factor ![]() :
:
A symbolic "Peaking" allpass filter with center frequency ![]() , quality factor
, quality factor ![]() , and gain value
, and gain value ![]() :
:
Use peak gain value of ![]() decibels:
decibels:
A symbolic "LowShelf" filter with center frequency ![]() , quality factor
, quality factor ![]() , and gain value
, and gain value ![]() :
:
Use low-shelf gain value of ![]() decibels:
decibels:
A symbolic "HighShelf" filter with center frequency ![]() , quality factor
, quality factor ![]() , and gain value
, and gain value ![]() :
:
Generalizations & Extensions (1)
Applications (1)
Properties & Relations (7)
Phase responses of the four basic filter types:
Extract the order of a BiquadraticFilterModel:
Stop-band attenuation increases by a factor of 40 decibels per decade:
Gain at cutoff frequency increases with increasing values of quality factor ![]() :
:
Width of bandpass filter decreases with increasing quality factor ![]() :
:
Gain values ![]() "boost" magnitude response of peaking equalizer:
"boost" magnitude response of peaking equalizer:
Gain values ![]() "cut" magnitude response of peaking equalizer:
"cut" magnitude response of peaking equalizer:
Gain values ![]() "boost" magnitude response of the low-shelf filter:
"boost" magnitude response of the low-shelf filter:
Gain values ![]() "cut" magnitude response of the low-shelf filter:
"cut" magnitude response of the low-shelf filter:
Related Guides
History
Text
Wolfram Research (2016), BiquadraticFilterModel, Wolfram Language function, https://reference.wolfram.com/language/ref/BiquadraticFilterModel.html.
CMS
Wolfram Language. 2016. "BiquadraticFilterModel." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BiquadraticFilterModel.html.
APA
Wolfram Language. (2016). BiquadraticFilterModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BiquadraticFilterModel.html
BibTeX
@misc{reference.wolfram_2025_biquadraticfiltermodel, author="Wolfram Research", title="{BiquadraticFilterModel}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/BiquadraticFilterModel.html}", note=[Accessed: 08-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_biquadraticfiltermodel, organization={Wolfram Research}, title={BiquadraticFilterModel}, year={2016}, url={https://reference.wolfram.com/language/ref/BiquadraticFilterModel.html}, note=[Accessed: 08-January-2026]}