BiquadraticFilterModel
BiquadraticFilterModel[{ω,q}]
特性周波数 ω とQ値 q を使ってローパス双二次フィルタを作る.
BiquadraticFilterModel[{"type",spec}]
指定された{"type",spec}のフィルタを作る.
BiquadraticFilterModel[{"type",spec},var]
モデルを変数 var によって表現する.
詳細

- 双二次フィルタは2つの二次多項式の比によって定義される二次フィルタで,アナログ・デジタル双方の信号処理回路で最もよく使われているものの一つである.
- BiquadraticFilterModelはフィルタをTransferFunctionModelとして返す.
- フィルタ指定{"type",spec}は次の任意のものでよい.
-
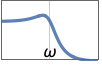
{"Lowpass",{{ω,q}}} カットオフ周波数 ω,Q値 q 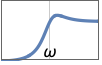
{"Highpass",{{ω,q}}} カットオフ周波数 ω,Q値 q 
{"Allpass",{{ω,q}}} 周波数 ω,Q値 q 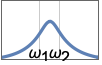
{"Bandpass",{ω1,ω2}} コーナー周波数 ω1と ω2 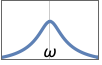
{"Bandpass",{{ω,q}}} 中心周波数 ω,Q値 q 
{"Bandstop",{ω1,ω2}} コーナー周波数 ω1と ω2 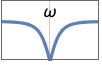
{"Bandstop",{{ω,q}}} 中心周波数 ω,Q値 q - 次のフィルタ指定を与えてイコライザを作ることができる.
-
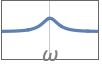
{"Peaking",{{ω,q}},g} ゲイン値 g を使ったピーキングイコライザ 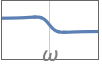
{"LowShelf",{{ω,q}},g} ゲイン値 g を使ったローパスシェルビングイコライザ 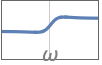
{"HighShelf",{{ω,q}},g} ゲイン値 g を使ったハイパスシェルビングイコライザ - ゲイン値
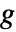 のとき,減衰は
のとき,減衰は 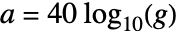 である.
である.
例題
すべて開くすべて閉じるスコープ (8)
特性と関係 (7)
BiquadraticFilterModelの次数を抽出する:
Wolfram Research (2016), BiquadraticFilterModel, Wolfram言語関数, https://reference.wolfram.com/language/ref/BiquadraticFilterModel.html.
テキスト
Wolfram Research (2016), BiquadraticFilterModel, Wolfram言語関数, https://reference.wolfram.com/language/ref/BiquadraticFilterModel.html.
CMS
Wolfram Language. 2016. "BiquadraticFilterModel." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BiquadraticFilterModel.html.
APA
Wolfram Language. (2016). BiquadraticFilterModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BiquadraticFilterModel.html