BohmanWindow[x]
represents a Bohman window function of x.


BohmanWindow
BohmanWindow[x]
represents a Bohman window function of x.
Details

- BohmanWindow is a window function typically used in signal processing applications where data needs to be processed in short segments.
- Window functions have a smoothing effect by gradually tapering data values to zero at the ends of each segment.
- BohmanWindow[x] is equal to
![ (-sin(2 pi x)+2 pi x cos(2 pi x)+pi cos(2 pi x))/pi -1/2<=x<0; (sin(2 pi x)-2 pi x cos(2 pi x)+pi cos(2 pi x))/pi 0<=x<=1/2; 0 TemplateBox[{x}, Abs]>1/2; (-sin(2 pi x)+2 pi x cos(2 pi x)+pi cos(2 pi x))/pi -1/2<=x<0; (sin(2 pi x)-2 pi x cos(2 pi x)+pi cos(2 pi x))/pi 0<=x<=1/2; 0 TemplateBox[{x}, Abs]>1/2;](Files/BohmanWindow.en/2.png) .
. - BohmanWindow automatically threads over lists.
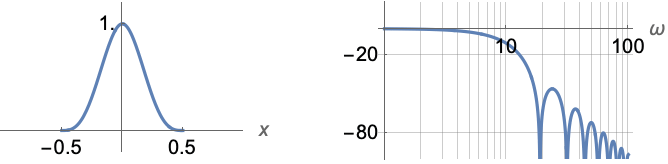
Examples
open all close allBasic Examples (3)
Scope (4)
Applications (3)
Create a moving-average filter of length 21:
Taper the filter using a Bohman window:
Log-magnitude plot of the power spectra of the filters:
Use a window specification to calculate sample PowerSpectralDensity:
Compare to spectral density calculated without a windowing function:
The plot shows that window smooths the spectral density:
Compare to the theoretical spectral density of the process:
See Also
Related Guides
History
Text
Wolfram Research (2012), BohmanWindow, Wolfram Language function, https://reference.wolfram.com/language/ref/BohmanWindow.html.
CMS
Wolfram Language. 2012. "BohmanWindow." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BohmanWindow.html.
APA
Wolfram Language. (2012). BohmanWindow. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BohmanWindow.html
BibTeX
@misc{reference.wolfram_2025_bohmanwindow, author="Wolfram Research", title="{BohmanWindow}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/BohmanWindow.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_bohmanwindow, organization={Wolfram Research}, title={BohmanWindow}, year={2012}, url={https://reference.wolfram.com/language/ref/BohmanWindow.html}, note=[Accessed: 09-March-2026]}