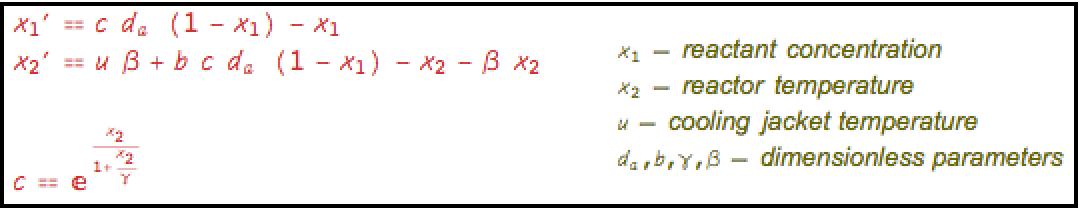CarlemanLinearize

CarlemanLinearize[sys,spec]

根据 spec 对非线性状态空间模型 sys 进行 Carleman 线性化.

更多信息

  • CarlemanLinearize 给出 sys 所嵌入的无限阶系统的逼近.
  • 输入线性系统的结果是双线性的，即在状态和输入都是线性的. 在一般情况下，它仅在状态是线性的.
  • spec 的可能值有：
  • k逼近阶
    {{e1,…,en}}嵌入变换的单项式
    {…,{z1,…,zn}}新状态变量
    {…,z,order}单项式排序
  • order 的可能设置与 MonomialList 中相同.
  • CarlemanLinearize 返回 LinearizingTransformationData 对象，可用于提取各种属性.
  • 可以给出下列属性：
  • "EmbeddingTransformation"{z1->e1,…,zn->en}
    "TransformedSystem"逼近变换系统
    {"OriginalSystemController",κ}原始系统 sys 的控制器
    {"OriginalSystemEstimator",ℓ}原始系统 sys 的估计器
    {"ClosedLoopSystem",κ}具有控制器的闭环系统 sys

范例

打开所有单元关闭所有单元

基本范例  (1)

对非线性系统进行 Carleman 线性化：

基于线性化模型设计控制器：

闭环系统：

模拟闭环系统：

范围  (10)

基本用法  (6)

对仿射系统进行 Carleman 线性化：

变换后系统是双线性的：

嵌入变换：

指定要用的新变量：

现在，结果是以指定变量的形式表示：

指定变换的形式：

指定排序：

直接指定属性：

直接指定多个属性：

NonlinearStateSpaceModel 的线性化：

变换后的系统在状态中是线性的：

属性  (4)

所有属性：

基本属性：

变换：

变换后的系统：

复合属性：

对系统线性化：

基于变换系统的泰勒线性化，设计控制器：

闭环系统是一个复合属性：

输出响应：

原始系统的控制器：

控制作用：

基于泰勒线性化设计的闭环系统：

系统的响应：

比较这两个响应：

使用 Carleman 线性化设计估计器：

变换后系统的一组估计器增益：

原始系统的估计器：

估计状态的轨迹：

实际状态轨迹：

比较实际和估计的状态轨迹：

应用  (2)

基于 Carleman 线性化设计一个用于治疗 HIV-1 感染的疗法. 参数为健康细胞的衰减率 和产率 ，感染率系数 ，和病毒的衰减率 ： »

状态是健康细胞的水平 和自由病毒 ，输入是药物剂量：

在目标水平为10时，低剂量将导致病毒水平提高：

对系统进行 Carleman 线性化：

为线性化高阶系统设计控制器：

闭环系统：

控制器将把健康细胞和病毒的浓度达到所需水平：

剂量水平：

使用 Carleman 线性化设计一个估计器，根据连续搅拌釜反应器（CSTR）中反应器的温度在来估计反应物浓度： »

组装模型，其中 为输入， 为状态：

对系统进行 Carleman 线性化：

设计估计器：

计算实际反应物浓度：

比较实际值和估计值：

属性和关系  (1)

阶数为1的 Carleman 线性化：

它等价于泰勒线性化：

Wolfram Research (2014)，CarlemanLinearize，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CarlemanLinearize.html.

文本

Wolfram Research (2014)，CarlemanLinearize，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CarlemanLinearize.html.

CMS

Wolfram 语言. 2014. "CarlemanLinearize." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/CarlemanLinearize.html.

APA

Wolfram 语言. (2014). CarlemanLinearize. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CarlemanLinearize.html 年

BibTeX

@misc{reference.wolfram_2024_carlemanlinearize, author="Wolfram Research", title="{CarlemanLinearize}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/CarlemanLinearize.html}", note=[Accessed: 23-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_carlemanlinearize, organization={Wolfram Research}, title={CarlemanLinearize}, year={2014}, url={https://reference.wolfram.com/language/ref/CarlemanLinearize.html}, note=[Accessed: 23-November-2024 ]}