Chebyshev2FilterModel

Chebyshev2FilterModel[n]

n 次のローパス第2種チェビシェフ(Chebyshev)フィルタを作る．

Chebyshev2FilterModel[{n,ωc}]

カットオフ周波数 ωc を使う．

Chebyshev2FilterModel[{"type",spec}]

完全なフィルタ指定{"type",spec}を使う．

Chebyshev2FilterModel[{"type",spec},var]

変数 var によってモデルを表す．

詳細

  • Chebyshev2FilterModelはフィルタをTransferFunctionModelとして与える．
  • Chebyshev2FilterModel[n]は，周波数 ω で減衰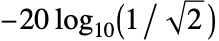（約3dB）のローパスフィルタを返す．
  • Chebyshev2FilterModel[n]は周波数1を使う．
  • フィルタ指定{"type",spec}には以下の任意のものを使うことができる．
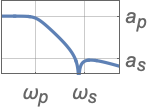
  • {"Lowpass",{ωp,ωs},{ap,as}}パスバンドとストップバンドの周波数と減衰を使ったローパスフィルタ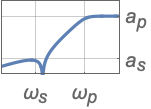
    {"Highpass",{ωs,ωp},{as,ap}}ハイパスフィルタ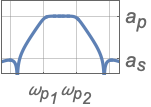
    {"Bandpass",{ωs1,ωp1,ωp2,ωs2},{as,ap}}バンドパスフィルタ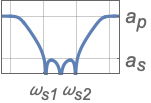
    {"Bandstop",{ωp1,ωs1,ωs2,ωp2},{ap,as}}バンドストップフィルタ
  • 周波数値は昇順で与えられなければならない．
  • 値 apと asはそれぞれパスバンドとストップバンドの減衰の絶対値である．
  • ゲインが 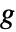のとき，減衰は 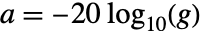である．

例題

すべて開くすべて閉じる

例  (1)

第2種チェビシェフフィルタモデル：

モデル化されたフィルタのボード線図：

スコープ  (7)

2次ローパスフィルタの記号表現：

モデルの厳密計算：

24桁精度でのモデルの計算：

変数sでフィルタモデルを作る：

ローパスの第2種チェビシェフフィルタを作る：

ハイパスの第2種チェビシェフフィルタを作る：

バンドパスの第2種チェビシェフフィルタを作る：

バンドストップの第2種チェビシェフフィルタを作る：

アプリケーション  (6)

ローパスの第2種チェビシェフフィルタを作る：

フィルタで正弦波信号から高周波ノイズを取り除く：

第2種チェビシェフフィルタの位相は，Arg[tf[ω ]]による応答を移動させる．この場合，ω は入力正弦曲線の周波数である：

位相のシフトを正す：

ローパスのプロトタイプからハイパスの第2種チェビシェフフィルタを作る：

フィルタで入力から低周波正弦曲線を取り除く：

次のパスバンド周波数，ストップバンド周波数，減衰を満足するて第2種チェビシェフ近似を使ってデジタルFIRローパスフィルタを設計する：

サンプリング周期が1であると仮定して，同等のアナログ周波数を得る：

アナログ第1種チェビシェフ伝達関数を計算する：

離散時間モデルに変換する：

離散時間第2種チェビシェフIIRフィルタのFIR近似を作る．

ローパスデジタル第2種チェビシェフフィルタを実装する：

IIRフィルタのインパルス応答を得，希望数のサンプルについて評価する：

FIRフィルタをプロットする：

チェビシェフフィルタのFIR近似を使って金融データを平滑化する：

ローパスの第2種チェビシェフフィルタを使って画像にフィルタをかける：

ハイパスの第2種チェビシェフフィルタを使って画像にフィルタをかける：

特性と関係  (5)

ローパスの第1種チェビシェフフィルタと第2種チェビシェフフィルタを比較する：

第2種多項式チェビシェフフィルタの次数を抽出する：

第2種チェビシェフフィルタの極と零点を求める：

チェビシェフフィルタの極と零点をプロットする：

ローパスデジタル第2種チェビシェフフィルタを実装する：

デジタル第2種チェビシェフフィルタの極と零点をプロットする：

ローパスフィルタをハイパスフィルタに変換する：

考えられる問題  (1)

記号フィルタは，次数が計算できないので，完全指定では返すことができない：

Wolfram Research (2012), Chebyshev2FilterModel, Wolfram言語関数， https://reference.wolfram.com/language/ref/Chebyshev2FilterModel.html.

テキスト

Wolfram Research (2012), Chebyshev2FilterModel, Wolfram言語関数， https://reference.wolfram.com/language/ref/Chebyshev2FilterModel.html.

CMS

Wolfram Language. 2012. "Chebyshev2FilterModel." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Chebyshev2FilterModel.html.

APA

Wolfram Language. (2012). Chebyshev2FilterModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Chebyshev2FilterModel.html

BibTeX

@misc{reference.wolfram_2024_chebyshev2filtermodel, author="Wolfram Research", title="{Chebyshev2FilterModel}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/Chebyshev2FilterModel.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_chebyshev2filtermodel, organization={Wolfram Research}, title={Chebyshev2FilterModel}, year={2012}, url={https://reference.wolfram.com/language/ref/Chebyshev2FilterModel.html}, note=[Accessed: 21-November-2024 ]}