DGaussianWavelet
二次導関数のガウス(Gauss)ウェーブレットの導関数を表す.
n 次導関数のガウスウェーブレットの導関数を表す.
詳細
- DGaussianWaveletは非直交ウェーブレット族を定義する.
- ウェーブレット関数(
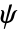 )は
)は![((-1)^(n+1))/(sqrt(TemplateBox[{{n, +, {1, /, 2}}}, Gamma])) (partial^n)/(partialx^n)exp(-(x^2)/2) ((-1)^(n+1))/(sqrt(TemplateBox[{{n, +, {1, /, 2}}}, Gamma])) (partial^n)/(partialx^n)exp(-(x^2)/2)](Files/DGaussianWavelet.ja/2.png) で与えられる.
で与えられる. - DGaussianWaveletはContinuousWaveletTransform,WaveletPsi等の関数で使うことができる.
例題
すべて開くすべて閉じるスコープ (2)
DGaussianWaveletを使ってContinuousWaveletTransformを行うことができる:
WaveletScalogramを使ってウェーブレット係数のタイムスケール表示を得ることができる:
InverseWaveletTransformを使って信号を再構築することができる:
特性と関係 (4)
DGaussianWavelet[2]はMexicanHatWaveletに等しい:
DGaussianWaveletはスケーリング関数を持たない:
Wolfram Research (2010), DGaussianWavelet, Wolfram言語関数, https://reference.wolfram.com/language/ref/DGaussianWavelet.html.
テキスト
Wolfram Research (2010), DGaussianWavelet, Wolfram言語関数, https://reference.wolfram.com/language/ref/DGaussianWavelet.html.
CMS
Wolfram Language. 2010. "DGaussianWavelet." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DGaussianWavelet.html.
APA
Wolfram Language. (2010). DGaussianWavelet. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DGaussianWavelet.html