Decompose[poly,x]
decomposes a polynomial, if possible, into a composition of simpler polynomials.


Decompose
Decompose[poly,x]
decomposes a polynomial, if possible, into a composition of simpler polynomials.
Details and Options
- Decompose gives a list of the polynomials Pi which can be composed as
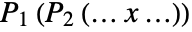 to give the original polynomial.
to give the original polynomial. - The set of polynomials Pi is not necessarily unique.
- Decomposition is an operation which is independent of polynomial factorization.
Examples
open all close allBasic Examples (3)
Scope (5)
Applications (1)
Solve some polynomial equations of degrees higher than 4 in terms of radicals:
Solve ![]() by solving
by solving ![]() and then
and then ![]() etc:
etc:
Check that these indeed are the roots of f:
Wolfram Language solvers use Decompose automatically:
Properties & Relations (2)
Composition of polynomials given by Decompose gives the original polynomial:
Use Fold to compose the polynomials:
Use Expand to show that the result is equal to f:
Use Factor to represent a polynomial as a product of irreducible factors:
f can be factored but not decomposed; g can be decomposed but not factored:
Possible Issues (1)
Decompose ignores possible decompositions with inner polynomials that are linear:
See Also
Tech Notes
Related Guides
History
Introduced in 1988 (1.0)
Text
Wolfram Research (1988), Decompose, Wolfram Language function, https://reference.wolfram.com/language/ref/Decompose.html.
CMS
Wolfram Language. 1988. "Decompose." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Decompose.html.
APA
Wolfram Language. (1988). Decompose. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Decompose.html
BibTeX
@misc{reference.wolfram_2025_decompose, author="Wolfram Research", title="{Decompose}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/Decompose.html}", note=[Accessed: 06-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_decompose, organization={Wolfram Research}, title={Decompose}, year={1988}, url={https://reference.wolfram.com/language/ref/Decompose.html}, note=[Accessed: 06-March-2026]}