f'
represents the derivative of a function f of one argument.
Derivative[n1,n2,…][f]
is the general form, representing a function obtained from f by differentiating n1 times with respect to the first argument, n2 times with respect to the second argument, and so on.


Derivative 
f'
represents the derivative of a function f of one argument.
Derivative[n1,n2,…][f]
is the general form, representing a function obtained from f by differentiating n1 times with respect to the first argument, n2 times with respect to the second argument, and so on.
Details

- f' is equivalent to Derivative[1][f].
- f'' evaluates to Derivative[2][f].
- You can think of Derivative as a functional operator which acts on functions to give derivative functions.
- Derivative is generated when you apply D to functions whose derivatives the Wolfram Language does not know.
- The Wolfram Language attempts to convert Derivative[n][f] and so on to pure functions. Whenever Derivative[n][f] is generated, the Wolfram Language rewrites it as D[f[#],{#,n}]&. If the Wolfram Language finds an explicit value for this derivative, it returns this value. Otherwise, it returns the original Derivative form.
- Derivative[-n][f] represents the n
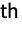 indefinite integral of f.
indefinite integral of f. - Derivative[{n1,n2,…}][f] represents the derivative of f[{x1,x2,…}] taken ni times with respect to xi. In general, arguments given in lists in f can be handled by using a corresponding list structure in Derivative.
- N[f'[x]] will give a numerical approximation to a derivative.
Examples
open all close allBasic Examples (1)
Scope (5)
The derivative of a function returns a function:
Partial derivatives with respect to different arguments:
The partial derivative with respect to the first argument:
A mixed partial evaluated at a particular value:
Partial derivatives for functions with list arguments:
The partial derivative with respect to the first element:
A mixed partial evaluated at a particular value:
Define a derivative for a function:
Define partial derivatives for a function:
Generalizations & Extensions (1)
Derivative with a negative integer order can do integrals:
Properties & Relations (1)
Use N to find a numerical approximation to the derivative:
Related Guides
Related Links
History
Introduced in 1988 (1.0) | Updated in 1996 (3.0) ▪ 1999 (4.0) ▪ 2000 (4.1) ▪ 2002 (4.2)
Text
Wolfram Research (1988), Derivative, Wolfram Language function, https://reference.wolfram.com/language/ref/Derivative.html (updated 2002).
CMS
Wolfram Language. 1988. "Derivative." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2002. https://reference.wolfram.com/language/ref/Derivative.html.
APA
Wolfram Language. (1988). Derivative. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Derivative.html
BibTeX
@misc{reference.wolfram_2025_derivative, author="Wolfram Research", title="{Derivative}", year="2002", howpublished="\url{https://reference.wolfram.com/language/ref/Derivative.html}", note=[Accessed: 08-September-2025]}
BibLaTeX
@online{reference.wolfram_2025_derivative, organization={Wolfram Research}, title={Derivative}, year={2002}, url={https://reference.wolfram.com/language/ref/Derivative.html}, note=[Accessed: 08-September-2025]}