DiscreteMarkovProcess[i0,m]
表示转移矩阵为 m 和初始状态为 i0 的离散时间有限状态马可夫过程.
DiscreteMarkovProcess[p0,m]
表示初始状态概率向量为 p0 的马可夫过程.
表示来自图 g 的转移矩阵的马可夫链.




DiscreteMarkovProcess
DiscreteMarkovProcess[i0,m]
表示转移矩阵为 m 和初始状态为 i0 的离散时间有限状态马可夫过程.
DiscreteMarkovProcess[p0,m]
表示初始状态概率向量为 p0 的马可夫过程.
表示来自图 g 的转移矩阵的马可夫链.
更多信息

- DiscreteMarkovProcess 也称为离散时间马可夫链.
- DiscreteMarkovProcess 是一个离散时间和离散状态随机过程.
- DiscreteMarkovProcess 的状态是位于 1 和
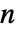 之间的整数,其中
之间的整数,其中 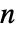 是转移矩阵 m 的长度.
是转移矩阵 m 的长度. - 转移矩阵 m 指定了条件转移概率 m〚i,j〛Probability[x[k+1]jx[k]i],其中 x[k] 是时间 k 处过程的状态. »
- 离散马可夫过程可以被视为图上的随机游走,其中从状态
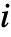 到状态
到状态 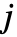 转移的概率由 m〚i,j〛 指定.
转移的概率由 m〚i,j〛 指定. - EstimatedProcess[data,DiscreteMarkovProcess[n]] 表示具有 n 个状态的过程应该被估计.
- 在图 g 中构建转移矩阵用来给出以相等概率转移至每个关联顶点.
- DiscreteMarkovProcess 中,m 是具有非负元素的
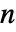 ×
×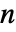 矩阵,其中各行之和为1,i0 是位于 1 和
矩阵,其中各行之和为1,i0 是位于 1 和 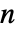 之间的整数,而 p0 是由和为 1 的非负元素组成的长度为
之间的整数,而 p0 是由和为 1 的非负元素组成的长度为 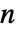 的向量.
的向量. - DiscreteMarkovProcess 可以与诸如 MarkovProcessProperties、PDF、Probability 和 RandomFunction 等函数一起使用.
范例
打开所有单元 关闭所有单元范围 (14)
应用 (18)
游戏 (7)
对重复投掷一个硬币的过程建模,使用离散马可夫过程,其中正面朝上的概率是 0.6,反面朝上的概率是 0.4:
一个正反面出现概率不同的硬币,正面朝上的概率是 ![]() ,将其投掷
,将其投掷 ![]() 次. 求连续正面朝上次数最多并且次数超过给定的
次. 求连续正面朝上次数最多并且次数超过给定的 ![]() 的概率. 这可以使用离散马可夫过程建模,其中状态
的概率. 这可以使用离散马可夫过程建模,其中状态 ![]() 表示连续出现
表示连续出现 ![]() 次正面朝上. 当
次正面朝上. 当 ![]() 、
、![]() 和
和 ![]() 时,转移矩阵如下所示:
时,转移矩阵如下所示:
模拟连续出现正面朝上的次数. 如果连续出现10次正面朝上,不重新开始计数:
在投掷硬币 100 次后,至少连续出现 10 次正面朝上的概率:
一个赌徒,从三个筹码开始,每一步下一个筹码,赢的概率是 0.4,目标是在破产前赢七个筹码. 状态是从 1 到 8 的整数,表示赌徒的财富加 1:
使用正反面概率相同的硬币,求出现序列“反正正”的马可夫过程:
使用正反面概率相同的硬币,求出现序列“正正正”的马可夫过程:
两个选手打网球,假设发球员赢一个点数的概率是 ![]() . 存在 17 种可能的状态:
. 存在 17 种可能的状态:
在掷骰子游戏中,玩家掷一对骰子并将点数相加. 第一次投掷时,如果他掷出 7 或者 11,则他获胜,如果掷出 2、3 或者 12 就输了,而任何其他数字称为一个点数,并且继续投掷. 在后面的投掷中,如果玩家掷出点数则获胜,如果掷出 7 则失败. 状态是:开始、赢、输、p4、p5、p6、p8、p9 或 p10. 他从不返回开始状态,而赢和输都是吸收状态. 下面的分布表示投掷一对骰子:
气候 (3)
一个简单的天气模型:给定今天下雨,明天也下雨的概率是 0.7;给定今天没有下雨,明天下雨的概率是 0.4. 给定今天下雨,使用离散马可夫过程表示该模型,求从今天开始下四天雨的概率. 天气的表示:
基于前两天是否下雨建立一个气候模型. 假设如果今天和昨天下雨,那么明天下雨的概率是 0.7,如果今天下雨但是昨天没有则概率为 0.5,如果昨天下雨今天没有,概率为 0.4,如果昨天或者今天都没下雨,概率是0.2. 使用产品状态空间 ![]() ,其中
,其中 ![]() 表明昨天是否下雨,
表明昨天是否下雨,![]() 表明今天是否下雨:
表明今天是否下雨:
的士要么在机场里,要么在城市中行驶. 从城市出发,下一站是机场的概率是 1/4,或者去城市另一个地方的概率是 3/4. 从机场出发,下一站总是到城市. 使用离散马可夫过程建模,状态1表示城市,状态2表示机场,从机场出发:
容器 (1)
随机游走 (2)
机器维修 (1)
保险 (1)
文本
Wolfram Research (2012),DiscreteMarkovProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DiscreteMarkovProcess.html (更新于 2014 年).
CMS
Wolfram 语言. 2012. "DiscreteMarkovProcess." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/DiscreteMarkovProcess.html.
APA
Wolfram 语言. (2012). DiscreteMarkovProcess. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DiscreteMarkovProcess.html 年
BibTeX
@misc{reference.wolfram_2025_discretemarkovprocess, author="Wolfram Research", title="{DiscreteMarkovProcess}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteMarkovProcess.html}", note=[Accessed: 18-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_discretemarkovprocess, organization={Wolfram Research}, title={DiscreteMarkovProcess}, year={2014}, url={https://reference.wolfram.com/language/ref/DiscreteMarkovProcess.html}, note=[Accessed: 18-February-2026]}