HiddenMarkovProcess[i0,m,em]
represents a discrete-time, finite-state hidden Markov process with transition matrix m, emission matrix em, and initial hidden state i0.
HiddenMarkovProcess[…,m,{dist1,…}]
represents a hidden Markov process with emission distributions disti.
HiddenMarkovProcess[p0,m,…]
represents a hidden Markov process with initial hidden state probability vector p0.


HiddenMarkovProcess
HiddenMarkovProcess[i0,m,em]
represents a discrete-time, finite-state hidden Markov process with transition matrix m, emission matrix em, and initial hidden state i0.
HiddenMarkovProcess[…,m,{dist1,…}]
represents a hidden Markov process with emission distributions disti.
HiddenMarkovProcess[p0,m,…]
represents a hidden Markov process with initial hidden state probability vector p0.
Details



- HiddenMarkovProcess is also known as a hidden Markov model or HMM.
- HiddenMarkovProcess is a discrete-time and discrete-state random process.
- A hidden Markov process has DiscreteMarkovProcess[p0,m] as an underlying hidden state transition process. The values observed from a hidden Markov process, called emissions, are random and follow emission distributions disti at state i. Emissions produced while visiting a given sequence of states are independent.
- The hidden states of HiddenMarkovProcess are integers between 1 and
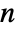 , where
, where 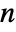 is the length of the transition matrix m.
is the length of the transition matrix m. - The transition matrix m specifies conditional hidden state transition probabilities m〚i,j〛Probability[x[k+1]jx[k]i], where x[k] is the hidden state of the process at time k.
- The emission matrix em specifies the probabilities for emissions at a given hidden state em〚i,r〛Probability[y[k]rx[k]i], where x[k] is the hidden state and y[k] is the emission at time k.
- The emission distributions disti must be all univariate or all multivariate, all discrete or all continuous.
- The emission distribution disti specifies that y[k]disti, given that x[k]i.
- A silent state that produces no emissions is represented by a row of zeros in the case of an emission matrix or by None for general emissions. Each silent state must have a path to an emitting state.
- For a hidden Markov process proc with silent states, HiddenMarkovProcess[proc] gives the effective process with silent states removed.
- EstimatedProcess[data,HiddenMarkovProcess[n,edist]] can be used to estimate an n state process with emission distributions in the family specified by edist.
- The following special edist templates can be used:
-
s s discrete emissions "Gaussian" Gaussian emissions dist emissions for all states distributed as dist {dist1,…,distn} emission distribution disti from state i - EstimatedProcess accepts the following settings for ProcessEstimator:
-
Automatic automatically choose the parameter estimator "BaumWelch" maximize log-likelihood by expectation maximization "ViterbiTraining" decode most likely path and use supervised training "StateClustering" use clustering followed by supervised training "SupervisedTraining" estimation using both state and emission data - The methods "BaumWelch", "ViterbiTraining", and "StateClustering" do not require specifying the hidden state path in the estimation, whereas "SupervisedTraining" relies on having access to the hidden state path data.
- Functions that work on data such as LogLikelihood accept Missing values.
- RandomFunction[HiddenMarkovProcess[…]] gives only emissions by default. With Method->{"IncludeHiddenStates"->True}, it gives a TemporalData object td with the state sequence included as metadata. The hidden state data can be retrieved using td["HiddenStates"].
- HiddenMarkovProcess allows m to be an
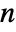 ×
×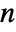 matrix with non-negative elements and rows that sum to 1, em an
matrix with non-negative elements and rows that sum to 1, em an 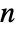 ×
×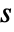 matrix with non-negative elements and rows that sum to 0 or 1, i0 an integer between 1 and
matrix with non-negative elements and rows that sum to 0 or 1, i0 an integer between 1 and 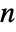 , and p0 a vector of length
, and p0 a vector of length 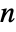 of non-negative elements that sum to 1.
of non-negative elements that sum to 1. - HiddenMarkovProcess can be used with such functions as LogLikelihood, FindHiddenMarkovStates, EstimatedProcess, PDF, Probability, and RandomFunction.
Examples
open all close allBasic Examples (2)
Scope (17)
Basic Usage (8)
Define a hidden Markov process with discrete emissions:
Define a hidden Markov process with continuous emissions:
Compute LogLikelihood of a sequence of emissions:
Define a hidden Markov process with continuous multivariate emissions:
Plot the probability density function of emission at time ![]() :
:
Define a hidden Markov process with silent states and discrete emissions:
Use None or a zero vector to denote silent states:
Find the most likely sequence of hidden states from the given emissions:
Find the effective hidden Markov process with silent states eliminated:
Define a hidden Markov process with silent states and continuous emissions:
Use None to denote silent states:
Find the effective hidden Markov process with silent states eliminated:
Estimate a hidden Markov process from data:
Specify a two-state process with three possible emission values:
Compute the covariance of a process:
Use a Graph annotated by Annotation to define HiddenMarkovProcess:
Estimation (5)
Estimate a two-state process with normally distributed emissions:
Overlay the histograms for the 100 paths:
Use the template form to specify the class of process to estimate:
Estimate a two‐state model with exponential emissions:
Provide a starting value for the process estimate:
Estimate the process using sv as an initial model:
Specify different estimation methods:
"BaumWelch" is the default estimator that iteratively maximizes the likelihood of given emissions:
"ViterbiTraining" is an iterative estimator that maximizes the joint likelihood of given emissions and their unknown underlying states:
"StateClustering" is commonly used to make a fast heuristic non‐iterative estimate:
Compare log‐likelihoods of estimated processes:
"SupervisedTraining" is an estimator that maximizes the joint likelihood of given emissions and given states:
Use the template form to specify the class of process to estimate:
Use the "StateData" suboption to specify data about underlying states for given emissions:
Estimate a three‐state model with two emissions and a silent state:
Estimate the model using a starting value process:
If no initial process is given, specify which states are silent in the template:
Process Slice Properties (4)
Find the PDF of the emission distribution at a fixed time:
Compute the mean and the covariance for symbolic times for multivariate emissions:
Sample emissions of the hidden Markov process at specified times:
Visualize frequencies and compare to theoretical results:
Find stationary distribution of emissions following a hidden Markov process:
Generalizations & Extensions (1)
Specify that RandomFunction should include the hidden state path:
The hidden states are stored as metadata in the produced TemporalData object:
Applications (11)
Games (3)
An occasionally dishonest casino offers a coin betting game and uses an unfair practice of using a biased coin for which the head is three times more likely than the tail. The casino dealer is known to secretly switch between the fair and biased coins with probability 10%:
The probabilities of getting heads or tails:
The resulting hidden Markov process, assuming equal probabilities of starting with either coin:
The probability of getting a head, given that the previous roll was a head:
If you intend to play six games, compute the probability that at least three tails will be tossed:
The probability if the casino is fair at all times:
Given a sequence of tosses, guess on which occasions the dealer used the biased coin:
There are three urns, each containing a large number of balls colored red, blue, and green:
Each time a person randomly selects an urn, selects a ball, announces the color, and returns the ball to one of the urns. The process is repeated four times. The probabilities of moving to the next urn are as follows:
The probabilities of picking a certain color from each urn correspond to the fraction of different balls for each urn:
Construct the hidden Markov process for the given probabilities of choosing the first urn:
The probability of getting the color sequence {red,blue,green,green}:
Given the color sequence, find the most likely sequence of urns that were picked:
In a first-person shooter game, an agent is hiding inside a level and waiting to jump out at the player. The agent cannot see the player but can hear what they are doing and can then match that against its knowledge of the layout to estimate the player’s position. Consider a layout with 27 regions of four types—grass, metal grates, water, and door portals:
Assign colors to the different types of regions:
Walking on the different terrain types produces different kinds of noises:
Probabilities of giving out noises depends on the terrain type:
Visualize the layout of the level:
Assume the player enters through one of the doors with equal probability:
The player remains in their current region with probability 10%, and otherwise is equally likely to move to any of the neighboring regions, giving the following transition probability matrix:
The agent hears the following sequence of noises:
This shows that most likely the player entered through the door marked 27 and is currently in region 7:
Genetics (3)
A DNA sequence consists of letters A, C, G, and T. Subsequences, called nucleotide sequences, are characterized by the frequency with which different letters occur. One important task is to split the sequences into their different nucleotide subsequences. Suppose you are given a sequence that begins in an exon, contains a 5' splice site, and ends in an intron. If the exons have a uniform base composition, the introns are deficient in C and G, and the splice site consensus nucleotide is a G with probability 0.95, the nucleotide frequency distributions are the following:
The state machine has states for exon (1), splice (2), intron (3), and end (4), with the following transition probabilities between states:
The emissions are nucleotides A (1), C (2), G (3), T (4), or end (5):
Find the most probable current nucleotide sequence (exon, splice, intron, or end):
The joint probability of the above nucleotide sequence and the DNA sequence:
Model breast cancer risk transmitted via a damaged allele B of the BRCA1 gene, with each parent contributing one of their alleles with probability 1/2 for each allele:
If the mother has a functional allele pair "bb", the probabilities of their son having each allele combination are:
The emission probabilities for the son are the same as for the father, since they are both male. The emission is 1 for cancer and 2 for no cancer:
Suppose you know the priors for the father:
Find the probability of both the father and the son developing breast cancer:
Two genes of a diploid plant are being investigated, having the following alleles:
There are nine distinct genotypes:
The plant is self‐pollinating, i.e. the genotype of its offspring depends on the genotype of the parent only:
Graph of genotype transitions between generations that encodes transition probabilities:
Model generational genotype changes using DiscreteMarkovProcess:
Alleles control the plant's phenotypes, i.e. visible features. Assuming complete dominance of capital letter alleles over respective lowercase letter alleles:
The genotypes control four distinct phenotypes:
The plant's phenotypes (indexed by an integer) are modeled by a hidden Markov process:
Simulate Mendel's observations, which he collected for 2734 plants over four generations:
Estimate genotype transition probabilities from these observations:
Linguistics (1)
Weather (2)
Tree ring sizes are well correlated with average annual temperatures. Using two temperature states (hot and cold) and three tree ring sizes (small, medium, and large), and given a four-year sequence of tree ring sizes ![]() , estimate the average annual temperature for those years. The transition probabilities for temperature switching:
, estimate the average annual temperature for those years. The transition probabilities for temperature switching:
The hidden Markov process model for tree ring sizes:
Find the most likely temperature sequence for the specific tree ring observations:
Find the sequence of the most likely individual temperatures:
Suppose you are locked in a room and your only clue as to the weather outside is whether or not the person bringing you your meals has an umbrella. The weather could be in one of three states—sunny, rainy, or foggy—with the following transition probabilities:
The probabilities of carrying an umbrella depending on the weather:
Model presence of umbrella by a hidden Markov process:
Inferences of the weather outside based on the pattern of clues:
Other (2)
A production process is in either in a good state or a poor state. When in a good state it remains so with probability 90%, and once it goes into a poor state it remains in that state forever:
When in a good state, the product quality is acceptable with probability 99%, and when in a poor state, the probability of acceptable quality product is 96%:
If the process starts in a good state with probability 80% and the first item was acceptable, find the probability of the next two produced items being of acceptable quality:
Consider a two-bit register with four possible states: 00, 01, 10, and 11. The register is initially in one of these four states with equal probabilities:
At each time step, the register is randomly manipulated. The register is left unchanged with probability 1/2, the two bits of the register are exchanged with probability 1/4, and the right bit is flipped with probability 1/4:
After the register has been manipulated in this fashion, the left bit is observed:
Given the first three observations to be 0, 0, and 1, find the most likely sequence of states:
Properties & Relations (6)
SliceDistribution of HiddenMarkovProcess with discrete emissions evaluates to an empirical DataDistribution:
Find distribution of emissions at time ![]() :
:
Find the PDF of the joint distribution of emissions at times ![]() and
and ![]() :
:
Emissions of HiddenMarkovProcess with exponential emissions at any single time follow HyperexponentialDistribution:
Emissions of HiddenMarkovProcess with generic emission distributions evaluate to MixtureDistribution:
An HMM with the identity as the emission matrix is equivalent to a discrete Markov process:
HiddenMarkovProcess is defined up to relabeling of hidden states:
Likelihoods of short emission sequences are the same for both processes:
Different hidden Markov models with silent states may assign identical likelihoods for all sequence emissions:
Verify that their effective hidden Markov processes are the same:
Check that likelihoods of all short emissions sequences in both models are the same:
Possible Issues (5)
The emission distributions must all have the same dimensionality:
The emission distributions must be either all discrete or all continuous:
The set of emitting states must be reachable from every silent state, i.e. no recurrent class may be entirely silent:
Modifying the transition probabilities makes the emitting state 1 accessible from silent state 2:
If the rows of the transition matrix do not sum to 1, they are automatically normalized:
If the initial probabilities do not sum to 1, they are normalized:
Related Guides
History
Text
Wolfram Research (2014), HiddenMarkovProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/HiddenMarkovProcess.html.
CMS
Wolfram Language. 2014. "HiddenMarkovProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HiddenMarkovProcess.html.
APA
Wolfram Language. (2014). HiddenMarkovProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HiddenMarkovProcess.html
BibTeX
@misc{reference.wolfram_2025_hiddenmarkovprocess, author="Wolfram Research", title="{HiddenMarkovProcess}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/HiddenMarkovProcess.html}", note=[Accessed: 07-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_hiddenmarkovprocess, organization={Wolfram Research}, title={HiddenMarkovProcess}, year={2014}, url={https://reference.wolfram.com/language/ref/HiddenMarkovProcess.html}, note=[Accessed: 07-March-2026]}