LogLikelihood

LogLikelihood[dist,{x1,x2,…}]

gives the log‐likelihood function for observations x1, x2, … from the distribution dist.

LogLikelihood[proc,{{t1,x1},{t2,x2},…}]

gives the log-likelihood function for the observations xi at time ti from the process proc.

LogLikelihood[proc,{path1,path2,…}]

gives the log-likelihood function for the observations from path1, path2, … from the process proc.

Details

  • The log‐likelihood function LogLikelihood[dist,{x1,x2,…}] is given by 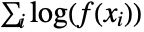, where 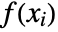is the probability density function at xi, PDF[dist,xi].
  • For a scalar‐valued process proc, the log-likelihood function LogLikelihood[proc,{{t1,x1},{t2,x2},…}] is given by LogLikelihood[SliceDistribution[proc,{t1,t2,…}],{{x1,x2,…}}].
  • For a vector‐valued process proc, the log-likelihood function LogLikelihood[proc,{{t1,{x1,…,z1},{t2,{x2,…,z2}},…}] is given by LogLikelihood[SliceDistribution[proc,{t1,t2,…}],{{x1,…,z1,x2,…,z2,…}}].
  • The log-likelihood function for a collection of paths LogLikelihood[proc,{path1,path2,…}] is given by 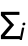sum_iLogLikelihood[proc,pathi].

Examples

open allclose all

Basic Examples  (4)

Get the log‐likelihood function for a normal distribution:

Compute a log‐likelihood for numeric data:

Plot log‐likelihood contours as a function of and :

Compute the log‐likelihood for multivariate data:

Compute the log-likelihood for a process:

Scope  (12)

Univariate Parametric Distributions  (2)

Compute the log‐likelihood for a continuous distribution:

Compute the log‐likelihood for a discrete distribution:

Plot the log‐likelihood, assuming is unknown:

Multivariate Parametric Distributions  (2)

Obtain the log‐likelihood for a continuous multivariate distribution with unknown parameters:

Visualize the log‐likelihood surface, assuming :

For a multivariate discrete distribution with known parameters:

Derived Distributions  (5)

Compute the log‐likelihood for a truncated standard normal:

Plot the log‐likelihood contours as a function of the truncation points:

Compute the log‐likelihood for a constructed distribution:

Compute the log‐likelihood for a product distribution:

Obtain the result as a sum of the independent componentwise log‐likelihoods:

Compute the log‐likelihood for a copula distribution:

Plot the log‐likelihood as a function of the kernel parameter:

Compute the log‐likelihood for a component mixture:

Random Processes  (3)

Compute the log-likelihood of a continuous parametric process:

Compute the log-likelihood of a scalar-valued discrete parametric process:

Plot the log‐likelihood as a function of the process parameter:

Compute the log-likelihood of a scalar-valued time series process:

Compute the log-likelihood of a vector-valued time series process:

Applications  (4)

Visualize the log‐likelihood surface for a distribution of two parameters:

Visualize as contours of equal log‐likelihood:

Show log-likelihood functions with mixed continuous and discrete parameters:

Solve for the Poisson maximum log-likelihood estimate in closed form:

Compute a maximum log-likelihood estimate directly:

Maximize:

Label the optimal point on a plot of the log-likelihood function:

Estimate the variance of the MLE estimator as the reciprocal of the expectation of second derivative of the log-likelihood function with respect to parameters:

Properties & Relations  (5)

LogLikelihood is the sum of logs of PDF values for data:

LogLikelihood is the log of Likelihood:

EstimatedDistribution estimates parameters by maximizing the log‐likelihood:

FindDistributionParameters gives the parameter estimates as rules:

Visualize the log‐likelihood function near the optimal value:

Log-likelihood of a process can be computed using its slice distribution:

Use the slice distribution:

For a vector-valued process:

Use the slice distribution:

Vectorize the path values for use in the LogLikelihood of the time slice distribution:

Given a sample from a distribution , the difference between values of LogLikelihood for and the MLE estimated distribution doubled is random and follows ChiSquareDistribution with degrees of freedom equal to the number of distribution parameters:

Draw samples from a 5-parameter binormal distribution in 1000 batches:

Compute the difference of log-likelihoods for each batch:

Check that the log-likelihood differences are consistent with ‐distribution:

Possible Issues  (1)

Log-likelihood of a continuous parametric process may be undefined:

This is due to degenerate slice distribution at time 0:

Start at positive time:

Neat Examples  (2)

Visualize isosurfaces for an exponential power log‐likelihood:

Visualize isosurfaces for a bivariate normal log‐likelihood:

Wolfram Research (2010), LogLikelihood, Wolfram Language function, https://reference.wolfram.com/language/ref/LogLikelihood.html (updated 2014).

Text

Wolfram Research (2010), LogLikelihood, Wolfram Language function, https://reference.wolfram.com/language/ref/LogLikelihood.html (updated 2014).

CMS

Wolfram Language. 2010. "LogLikelihood." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/LogLikelihood.html.

APA

Wolfram Language. (2010). LogLikelihood. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LogLikelihood.html

BibTeX

@misc{reference.wolfram_2024_loglikelihood, author="Wolfram Research", title="{LogLikelihood}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/LogLikelihood.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_loglikelihood, organization={Wolfram Research}, title={LogLikelihood}, year={2014}, url={https://reference.wolfram.com/language/ref/LogLikelihood.html}, note=[Accessed: 21-November-2024 ]}