is an option to EstimatedProcess and FindProcessParameters that specifies what process parameter estimator to use.


ProcessEstimator
is an option to EstimatedProcess and FindProcessParameters that specifies what process parameter estimator to use.
Details and Options

- The following basic settings can be used:
-
Automatic automatically choose the estimator to use "MaximumLikelihood" maximize the log‐likelihood function - The maximum likelihood method will maximize the log-likelihood function
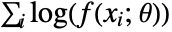 , where
, where 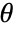 is the process parameters and
is the process parameters and 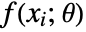 is the PDF for the joint SliceDistribution of the
is the PDF for the joint SliceDistribution of the 
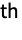 path.
path. - ProcessEstimator->{"estimator",Method->"solver"} specifies what underlying optimization solver to use.
- Possible solver settings for "MaximumLikelihood" include:
-
Automatic automatically chosen solver "FindMaximum" use FindMaximum to maximize log-likelihood "NMaximize" use NMaximize to maximize log-likelihood - With the setting ProcessEstimator->{"estimator",Method->{"solver",opts}}, additional options can be given for the solver.
- Solver methods such as NMaximize that do not rely on starting values will not make use of starting values given to EstimatedProcess or FindProcessParameters.
- Special settings for ProcessEstimator are documented under the individual random process reference pages.
See Also
Related Guides
History
Text
Wolfram Research (2012), ProcessEstimator, Wolfram Language function, https://reference.wolfram.com/language/ref/ProcessEstimator.html.
CMS
Wolfram Language. 2012. "ProcessEstimator." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ProcessEstimator.html.
APA
Wolfram Language. (2012). ProcessEstimator. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ProcessEstimator.html
BibTeX
@misc{reference.wolfram_2025_processestimator, author="Wolfram Research", title="{ProcessEstimator}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/ProcessEstimator.html}", note=[Accessed: 28-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_processestimator, organization={Wolfram Research}, title={ProcessEstimator}, year={2012}, url={https://reference.wolfram.com/language/ref/ProcessEstimator.html}, note=[Accessed: 28-February-2026]}