WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

DiscreteVariables

NDSolveおよびその他の関数のオプションで，時間積分で離散時間でのみ変化する変数を指定する．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
アプリケーション  
特性と関係  
考えられる問題  
関連項目
関連するガイド
履歴
引用書式

DiscreteVariables

DiscreteVariables

NDSolveおよびその他の関数のオプションで，時間積分で離散時間でのみ変化する変数を指定する．

詳細

  • DiscreteVariables->{v1, v2,…}は，v1, v2, …を離散時間でのみ変化する変数として扱うように指定する．
  • 離散変数 v の値はWhenEvent[event,v->val]あるいはWhenEvent[event,v->"DiscontinuitySignature"]を通して変えることができる．
  • 離散変数解 v はNDSolve[eqn,{v,…},…]を使って返すことができる．
  • DiscreteVariables->{vspec1,vspec2,…}を使って離散変数の範囲を指定することができる．
  • vspeciの可能な形式
  • vv の領域はRealsまたはComplexes
    Element[v,Reals]v の領域はReals
    Element[v,Complexes]v の領域はComplexes
    Element[v,Integers]v の領域はIntegers
    Element[v,{n1,…}]v は離散範囲{n1,…}を持つ
    {v,vmin,vmax}v の範囲は 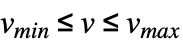v_(min)<=v<=v_(max)である
    vspeciactionivspeci が満たされなくなったときに actioniを実行する
  • 離散変数の時間についての導関数は，ほぼあらゆるところでゼロであり，方程式に使われるべきではない．
  • 偏微分方程式では，離散変数は半離散化の線の方法における時間独立変数にのみ依存することができる．

例題

すべて開く すべて閉じる

例  (2)

について時間的に一定の間隔で変化する離散変数である を使って解く：

Wolfram Language code: sol = NDSolve[{y'[t] == a[t], WhenEvent[Mod[t, 1], a[t] -> y[t]], y[0] == 1, a[0] == 1}, {y, a}, {t, 0, 4}, DiscreteVariables -> {a}]
Wolfram Language code: Plot[Evaluate[{y[t], a[t]} /. sol], {t, 0, 4}]

について が0と交差するたびに変化する離散変数である を使って解く：

Wolfram Language code: sol = NDSolve[{y''[t] + a[t]y[t] == 0, WhenEvent[y[t], a[t] -> a[t] + 1], y[0] == 1, y'[0] == 0, a[0] == 1}, {y, a}, {t, 0, 20}, DiscreteVariables -> a]
Wolfram Language code: Plot[y[t] /. sol, {t, 0, 20}]
Wolfram Language code: Plot[a[t] /. sol, {t, 0, 20}]

スコープ  (7)

一定の時間間隔で離散変数を増分する：

Wolfram Language code: sol = NDSolve[{y'[t] == a[t], y[0] == 0, a[0] == 0, WhenEvent[Mod[t, 1], a[t] -> a[t] + 1]}, {y, a}, {t, 0, 4}, DiscreteVariables -> a];
Wolfram Language code: Plot[Evaluate[{y[t], a[t]} /. sol], {t, 0, 4}]

解が0と交差するときに離散変数を増分する：

Wolfram Language code: sol = NDSolve[{y''[t] == -y[t], y[0] == y'[0] == 1, a[0] == 0, WhenEvent[y[t] == 0, a[t] -> a[t] + 1]}, {y, a}, {t, 0, 10}, DiscreteVariables -> a];
Wolfram Language code: Plot[Evaluate[{y[t], a[t]} /. sol], {t, 0, 10}]

解が0と交差するときに複数の離散変数を同時に変更する：

Wolfram Language code: eqns = {y''[t] + .5 b[t]y'[t] == -a[t]y[t], a[0] == y[0] == y'[0] == 1, b[0] == 2};
Wolfram Language code: sol1 = NDSolve[{eqns, WhenEvent[y[t] == 0, {a[t], b[t]} -> {a[t] + 1, b[t] + a[t]}]}, {y, a, b}, {t, 0, 8}, DiscreteVariables -> {a, b}];
Wolfram Language code: Plot[Evaluate[{y[t], a[t], b[t]} /. sol1], {t, 0, 8}]

今回は， を変更する前に の変更を実施する：

Wolfram Language code: sol2 = NDSolve[{eqns, WhenEvent[y[t] == 0, {a[t] -> a[t] + 1, b[t] -> b[t] + a[t]}]}, {y, a, b}, {t, 0, 8}, DiscreteVariables -> {a, b}];
Wolfram Language code: Plot[Evaluate[{y[t], a[t], b[t]} /. sol2], {t, 0, 10}]

離散変数が離散範囲{1,2,3}の外に出たときに積分を中止する：

Wolfram Language code: eqns = {x''[t] == -x[t], x[0] == 1, x'[0] == 0, a[0] == 1, WhenEvent[x[t], a[t] -> a[t] + 1]};
Wolfram Language code: NDSolve[eqns, x[t], {t, 0, 10}, DiscreteVariables -> {a[t]∈{1, 2, 3}}]

離散変数に連続的な範囲の外に出たときに積分を中止する：

Wolfram Language code: NDSolve[eqns, x[t], {t, 0, 10}, DiscreteVariables -> {{a[t], 0, 3}}]

変数が範囲外に出た場合にメッセージを表示するが，方程式の積分は続行する：

Wolfram Language code: NDSolve[eqns, x, {t, 0, 10}, DiscreteVariables -> {a[t]∈{1, 3, 5, 7} :> Print[{a[t], t}]}]

この初期条件もまた範囲外である：

Wolfram Language code: NDSolve[eqns, x, {t, 0, 10}, DiscreteVariables -> {a[t]∈{2, 3} :> Print[{a[t], t}]}]

離散変数は数値以外の値も取ることができる：

Wolfram Language code: NDSolve[{y'[t] == Switch[a[t], up, 1, down, -1], y[0] == 0, a[0] == up, WhenEvent[y[t] ^ 2 - 1 == 0, a[t] -> Switch[a[t], up, down, down, up]]}, y, {t, 0, 10}, DiscreteVariables -> {a[t]∈{up, down}}];
Wolfram Language code: Plot[y[t] /. %, {t, 0, 10}]

アクション"DiscontinuitySignature"を用いてスライディングモードによる解が得られるようにする：

Wolfram Language code: sol = NDSolve[{y'[t] == -a[t], y[0] == -1, a[0] == -1, WhenEvent[y[t], a[t] -> "DiscontinuitySignature"]}, {y, a}, {t, 0, 5}, DiscreteVariables -> {a[t]∈{-1, 0, 1}}];

ベクトル場と解をプロットする：

Wolfram Language code: vf = VectorPlot[{1, -Sign[y]}, {x, 0, 5}, {y, -1, 1}, VectorColorFunction -> None, VectorStyle -> {Gray, Arrowheads[.04]}, VectorPoints -> 10, FrameLabel -> {t, y}];
Wolfram Language code: Show[vf, Plot[y[t] /. sol, {t, 0, 5}, PlotRange -> {-1, 1}, PlotStyle -> {Red}]]

解がスライディングモードのとき，離散変数 の値は0である：

Wolfram Language code: Plot[a[t] /. sol, {t, 0, 5}]

がスライディング不連続曲線 に達したときに不連続状態変数 を設定する：

Wolfram Language code: c[t_] = Sin[t];
Wolfram Language code: sol = NDSolve[{Derivative[1][x][t] == 1, Derivative[1][y][t] == -v[t], WhenEvent[y[t] - c[t], v[t] -> "DiscontinuitySignature"], x[0] == 0, y[0] == .5, v[0] == 1}, {x, y, v}, {t, 0, 6}, DiscreteVariables -> {v∈{-1, 0, 1}}];
Wolfram Language code: curve = Plot[c[x], {x, 0, 2}, PlotStyle -> Red];
Wolfram Language code: Show[curve, ParametricPlot[{{x[t], y[t]}} /. sol, {t, 0, 2}]]

アプリケーション  (5)

離散変数を使って微分方程式の2つの右辺を切り換える：

Wolfram Language code: rhs[t_, x_, 1] = -x; rhs[t_, x_, 2] = 1;
Wolfram Language code: sol = NDSolve[{x'[t] == rhs[t, x[t], a[t]], x[0] == 1, a[0] == 1, WhenEvent[x[t] - .1, a[t] -> 2], WhenEvent[x[t] - 2, a[t] -> 1]}, {x, a}, {t, 0, 15}, DiscreteVariables -> {a[t]∈{1, 2}}];
Wolfram Language code: Plot[x[t] /. sol, {t, 0, 10}]

複数の右辺を切り換える微分方程式を設定する：

Wolfram Language code: Do[rhs[t_, x_, i] = t RandomReal[{-.1, .1}] + x RandomReal[{-1, 1}] + RandomReal[{-.1, .1}], {i, 11}]
Wolfram Language code: NDSolve[{x'[t] == rhs[t, x[t], a[t]], x[0] == 0, a[0] == 1, WhenEvent[Mod[t, 1], a[t] -> a[t] + 1]}, x, {t, 0, 10}, DiscreteVariables -> {a[t]∈Range[11]}];
Wolfram Language code: Plot[x[t] /. %, {t, 0, 10}]

階段を弾みながら転がっていくボールのシミュレーションを行う：

Wolfram Language code: c = .75; xsol = NDSolve[{y''[t] == -9.8, y[0] == 13.5, y'[0] == 5, a[0] == 13, WhenEvent[y[t] - a[t] == 0, y'[t] -> -c y'[t]], WhenEvent[Mod[t, 1], a[t] -> a[t] - 1]}, {y, a}, {t, 0, 8}, DiscreteVariables -> {a}] ;
Wolfram Language code: Plot[Evaluate[{y[t], a[t]} /. xsol], {t, 0, 8}, Filling -> {2 -> 0}]

ボールの運動，ポテンシャル，総エネルギーをプロットする：

Wolfram Language code: kin[v_] := .5 v ^ 2; pot[y_] := 9.8y; energy[y_, v_] := kin[v] + pot[y];
Wolfram Language code: Plot[Evaluate[{kin[y'[t]], pot[y[t]], energy[y[t], y'[t]]} /. xsol], {t, 0, 8}]

離散時間コントローラ で安定化された の系のシミュレーションを行う：

Wolfram Language code: τ = 1.0; sol = NDSolve[{y'[t] == y[t] + u[t], y[0] == 1, u[0] == 0, WhenEvent[Mod[t, τ], u[t] -> -2y[t]]}, {y, u}, {t, 0, 20}, DiscreteVariables -> u];
Wolfram Language code: Plot[Evaluate[{u[t], y[t]} /. sol], {t, 0, 10}, PlotRange -> {-6, 6}]

波動方程式の における波の速さ を変える：

Wolfram Language code: sol = NDSolve[{Subscript[∂, t, t]u[t, x] == a[t]Subscript[∂, x, x]u[t, x], u[0, x] == E^-x^2, u^(1, 0)[0, x] == 0, u[t, -10] == u[t, 10], a[0] == 1, WhenEvent[Mod[t, 1], a[t] -> Sqrt[t]]}, u, {t, 0, 40}, {x, -10, 10}, DiscreteVariables -> {a[t]}];
Wolfram Language code: DensityPlot[Evaluate[First[u[t, x] /. sol]], {t, 0, 40}, {x, -10, 10}, PlotPoints -> 50]

特性と関係  (1)

NDSolveは離散変数を使って，Signのような不連続関数を自動的に処理する：

Wolfram Language code: sol1 = NDSolve[{y'[t] == Sign[1 - y[t]], y[0] == 0}, y, {t, 0, 2}];
Wolfram Language code: Plot[y[t] /. sol1, {t, 0, 2}]

"DiscontinuitySignature"を離散変数と一緒に使ってSign関数を模倣する：

Wolfram Language code: sol2 = NDSolve[{Derivative[1][y][t] == a[t], WhenEvent[1 - y[t], a[t] -> "DiscontinuitySignature"], y[0] == 0, a[0] == 1}, y, {t, 0, 2}, DiscreteVariables -> {a∈{-1, 0, 1}}];
Wolfram Language code: Plot[y[t] /. sol2, {t, 0, 2}]

考えられる問題  (3)

離散変数が範囲外に出ると，メッセージが表示され積分が中止される：

Wolfram Language code: NDSolve[{x''[t] == -x[t], x[0] == 1, x'[0] == 0, y[0] == 0, WhenEvent[x[t], y[t] -> y[t] + 1]}, {x, y}, {t, 0, 8}, DiscreteVariables -> {{y[t], 0, 2}}]

離散変数の導関数は，NDSolveに渡される方程式に含まれていてはならない：

Wolfram Language code: NDSolve[{x''[t] == -a'[t] x[t], x[0] == 1, x'[0] == 0, a[0] == 0, WhenEvent[x[t], a[t] -> a[t] + 1]}, {x, a}, {t, 0, 8}, DiscreteVariables -> {{a[t], 0, 2}}]

"DiscontinuitySignature"アクションのある離散変数の範囲は{-1,0,1}でなければならない：

Wolfram Language code: sol = NDSolve[{Derivative[1][y][t] == a[t], WhenEvent[1 - y[t], a[t] -> "DiscontinuitySignature"], y[0] == 0, a[0] == 1}, y, {t, 0, 2}, DiscreteVariables -> {a∈{-2, -1, 0, 1}}];

範囲が{-1,1}の場合は，スライディングモード解は求まらない：

Wolfram Language code: sol = NDSolve[{Derivative[1][y][t] == a[t], WhenEvent[1 - y[t], a[t] -> "DiscontinuitySignature"], y[0] == 0, a[0] == 1}, y, {t, 0, 2}, DiscreteVariables -> {a∈{-1, 1}}];
Wolfram Language code: Plot[{y[t] /. sol}, {t, 0, 2}]

スライディングモード解を求めるためには，範囲をElement[a,{-1,0,1}]として指定する：

Wolfram Language code: sol = NDSolve[{Derivative[1][y][t] == a[t], WhenEvent[1 - y[t], a[t] -> "DiscontinuitySignature"], y[0] == 0, a[0] == 1}, y, {t, 0, 2}, DiscreteVariables -> {a∈{-1, 0, 1}}];
Wolfram Language code: Plot[{y[t] /. sol}, {t, 0, 2}]
Wolfram Research (2012), DiscreteVariables, Wolfram言語関数， https://reference.wolfram.com/language/ref/DiscreteVariables.html.

テキスト

Wolfram Research (2012), DiscreteVariables, Wolfram言語関数， https://reference.wolfram.com/language/ref/DiscreteVariables.html.

CMS

Wolfram Language. 2012. "DiscreteVariables." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteVariables.html.

APA

Wolfram Language. (2012). DiscreteVariables. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteVariables.html

BibTeX

@misc{reference.wolfram_2026_discretevariables, author="Wolfram Research", title="{DiscreteVariables}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteVariables.html}", note=[Accessed: 20-July-2026]}

BibLaTeX

@online{reference.wolfram_2026_discretevariables, organization={Wolfram Research}, title={DiscreteVariables}, year={2012}, url={https://reference.wolfram.com/language/ref/DiscreteVariables.html}, note=[Accessed: 20-July-2026]}