DivisorSigma

DivisorSigma[k,n]

約数関数 を返す．

詳細とオプション

  • DivisorSigmaは，約数関数あるいは約数の和の関数としても知られている．
  • 記号操作・数値操作の両方に適した数学的整数関数である．
  • DivisorSigma[k,n]は n の約数の k 次ベキの和である．
  • 数 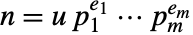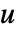（ は単元で は素数）について，DivisorSigma[k,n]は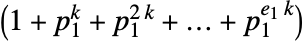を返す．
  • GaussianIntegers->Trueのとき，DivisorSigmaはガウス整数である約数を含む．
  • DivisorSigma[k,m+In]は自動的にガウス整数上で作用する．

例題

すべて開くすべて閉じる

例  (2)

の約数を求める：

約数の和：

約数の二乗の和：

DivisorSigmaを対数スケールの値でプロットする：

スコープ  (12)

数値評価  (4)

DivisorSigmaは整数に使うことができる：

負のベキ乗：

有理数のベキ乗：

ガウス整数：

大きい整数について計算する：

DivisorSigmaは要素単位でリストに縫い込まれる：

記号演算  (8)

TraditionalFormによる表示：

簡約された式：

方程式を解く：

式を簡約する：

総和の中でDivisorSigmaを使う：

DirichletTransform：

記号引数について計算する：

関数を生成する：

オプション  (1)

GaussianIntegers  (1)

の約数の和を整数上で求める：

ガウス整数：

アプリケーション  (13)

基本的なアプリケーション  (3)

一般にDivisorSigma[d,n]=∑k|nkdである：

ガウスの約数と整数の約数の割合：

DivisorSigmaを対数スケールの値でプロットする：

特殊数列  (4)

完全数（約数の和が になるような数 n）を認識する：

不足数（約数の和が よりも小さくなるような数 n）：

過剰数（約数の和が よりも大きくなるような数 n）：

高度に合成された数を認識する [詳細]：

友愛数（異なる2つの数．各々の真の約数の和がもう一方の数と等しい）を認識する：

-倍積完全数（約数の和が である数）を認識する：

最初の -完全数はである：

-完全である数は完全数と呼ばれる：

整数論  (6)

n がのベキ乗なら，n の約数の和はになるが，これは n を概完全数にする：

ある数が完全平方のときかつそのときにかぎり，約数の数は奇数である：

オイラー(Euler)のトーシェント関数と約数の数を比較する：

約数の数の移動平均をその漸近値とともにプロットする：

反復するアリコット合計を計算する：

極限の進化を示す：

特性と関係  (6)

DivisorSigmaは，約数の 次ベキの和である：

DivisorSumを使って約数の和を求める：

DivisorSigmaは乗法的関数である：

完全数 n 約数の逆数はまででなければならない：

素数ベキ n の約数の和は2n 未満である：

素数 p について，約数の数はである：

約数の和は である：

の約数の数は である：

DivisorSigmaを使って約数の積を求める：

考えられる問題  (1)

GaussianIntegers->Trueのとき，ネイティブな定義では正しい結果が出ない：

DivisorSigmaを倍に増える関数にするために，因数を含む定義が使用されている：

おもしろい例題  (4)

DivisorSigmaのフーリエ変換の引数をプロットする：

DivisorSigmaのフーリエ変換の絶対値をプロットする：

DivisorSigmaのフーリエ変換の引数をプロットする：

約数の平均のウラム(Ulam)螺線をプロットする：

Wolfram Research (1988), DivisorSigma, Wolfram言語関数， https://reference.wolfram.com/language/ref/DivisorSigma.html.

テキスト

Wolfram Research (1988), DivisorSigma, Wolfram言語関数， https://reference.wolfram.com/language/ref/DivisorSigma.html.

CMS

Wolfram Language. 1988. "DivisorSigma." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DivisorSigma.html.

APA

Wolfram Language. (1988). DivisorSigma. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DivisorSigma.html

BibTeX

@misc{reference.wolfram_2024_divisorsigma, author="Wolfram Research", title="{DivisorSigma}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/DivisorSigma.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_divisorsigma, organization={Wolfram Research}, title={DivisorSigma}, year={1988}, url={https://reference.wolfram.com/language/ref/DivisorSigma.html}, note=[Accessed: 21-November-2024 ]}