EstimatedPointNormals

EstimatedPointNormals[{p1,p2,…}]

点 p1,p2,…の法線ベクトルを推定する．

EstimatedPointNormals[mreg]

メッシュ領域 mreg の頂点の法線ベクトルを推定する．

詳細とオプション

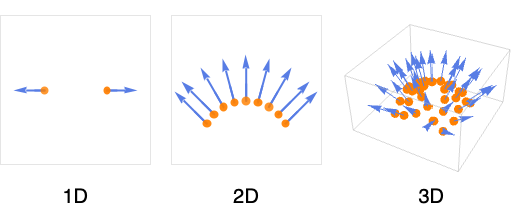
  • EstimatedPointNormalsは，通常，点の集合から超曲面の方向を求めるために使われる．
  • EstimatedPointNormals[{p1,p2,…}]はリスト{n1,n2,…}を与える．ここで，niは piの単位法線ベクトルである．
  • EstimatedPointNormals[{p1,p2,…}]の piは座標または明示的なPointオブジェクトのリストでよい．
  • Methodオプションも与えられる．次は，使用可能なMethod設定である．
  • "PlaneFitting"最近傍を使った平面フィット
    "FaceWeighted"重み付き面の法線

例題

すべて開くすべて閉じる

例  (3)

円上の点の推定法線：

球上の点の推定法線：

曲面をランダムにサンプリングすることで点のクラウドを生成する：

推定法線を照明付きで可視化する：

スコープ  (2)

基本的な用法  (1)

1Dの点の推定法線：

2D：

3D：

D：

指定  (1)

EstimatedPointNormalsは点の集合を取る：

Pointのリストを使う：

アプリケーション  (3)

基本的なアプリケーション  (1)

滑らかな曲面の十分に密なサンプリングを与えられた場合に，空間的に近くにあるサンプルは曲面上でも近くにあると考えることができる：

各点の周りの局所的な曲面は，したがって，点の最近傍からサンプルを取ったものである：

局所的な曲面はそのサンプル点にフィットされた平面で近似できる：

これらのフィットされた平面の法線は対応する点の推定法線として使うことができる：

点群描画  (1)

照明の計算に推定された法線を使って点群を描画する：

描画された点群をグラウンドトゥルースモデルと比較する：

表面再構成  (1)

表面再構成の際に使用する法線を推定する：

特性と関係  (2)

EstimatedPointNormalsは表面再構成のために法線が生成できる：

もとになっている関数が分からなければ偏微分を使って直接法線ベクトルを計算することができる：

インタラクティブな例題  (1)

ドラッグ可能な点で法線がリアルタイムで更新されるようなインタラクティブな例題を作成する：

おもしろい例題  (1)

推定される法線の方向に基づいて点群に色を割り当てる：

Wolfram Research (2022), EstimatedPointNormals, Wolfram言語関数， https://reference.wolfram.com/language/ref/EstimatedPointNormals.html.

テキスト

Wolfram Research (2022), EstimatedPointNormals, Wolfram言語関数， https://reference.wolfram.com/language/ref/EstimatedPointNormals.html.

CMS

Wolfram Language. 2022. "EstimatedPointNormals." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/EstimatedPointNormals.html.

APA

Wolfram Language. (2022). EstimatedPointNormals. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EstimatedPointNormals.html

BibTeX

@misc{reference.wolfram_2024_estimatedpointnormals, author="Wolfram Research", title="{EstimatedPointNormals}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/EstimatedPointNormals.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_estimatedpointnormals, organization={Wolfram Research}, title={EstimatedPointNormals}, year={2022}, url={https://reference.wolfram.com/language/ref/EstimatedPointNormals.html}, note=[Accessed: 17-November-2024 ]}