RegionFit

RegionFit[{p1,p2,…},"model"]

finds a geometric region "model" that best fits the points p1,p2,….

RegionFit[{p1,p2,…},"model","prop"]

specifies what fit property "prop" should be returned.

Details and Options

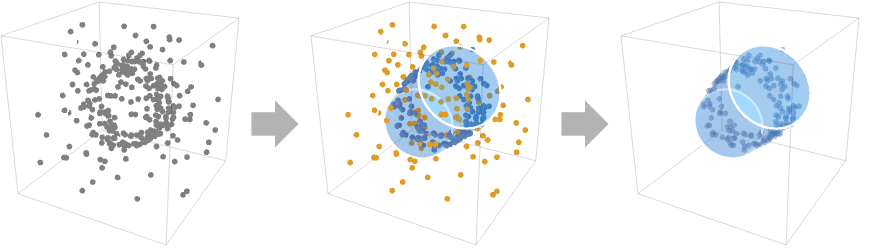
  • RegionFit is also known as sample consensus model.
  • RegionFit is typically used for fitting and reconstructing regions from a set of points.
  • RegionFit[{p1,p2,…},"model"] finds a region that contains the most points pi by iteratively estimating parameters of the specified "model" from a set of points.
  • Possible 2D "model" specifications include:
  • "Line"infinite line
    "Circle"circle
  • Possible 3D "model" specifications include:
  • "Line"infinite line
    "Circle"circle
    "Plane"plane
    "Sphere"sphere
    "Cylinder"cylinder
    "Cone"cone
  • RegionFit[Point[{p1,p2,…}]] is effectively equivalent to RegionFit[{p1,p2,…}].
  • Vertex normals ni for points pi can be specified by Point[{p1,p2,…},VertexNormals{n1,n2,…}].
  • RegionFit[{p1,p2,…},"model","prop"] returns the value of the fit property "prop".
  • Possible fit properties "prop" include:
  • "BestFit"the best candidate model
    "Points"set of points
    "Inliers"points fitting the candidate model
    "Outliers"points not fitting the candidate model
    "DistanceVariance"variance of distances to the candidate model
    "Distances"distances to the best candidate model
    {prop1,prop2,…}several fit properties
  • The following options can be given:
  • ConfidenceLevelAutomaticdesired probability of outlier-free sample
    MethodAutomaticmethod to use
    PerformanceGoal$PerformanceGoalaspects of performance to try to optimize
    Tolerance Automaticnumerical tolerance to use
    VertexNormalsNonevertex normals for points
    WorkingPrecision Automaticprecision to use in computations
  • Possible settings for Method include:
  • "RANSAC"random sample consensus
    "LMEDS"least median of squares
    "MSAC"M-estimator sample consensus
    "RRANSAC"randomized RANSAC
    "RMSAC"randomized MSAC
    "MLESAC"maximum likelihood estimation sample consensus
    "PROSAC"progressive sample consensus

Examples

open allclose all

Basic Examples  (2)

Find a circle that fits a set of points:

Show the fit:

A set of points with many outliers fitted by a cylinder:

Visualize the fitted region with the data:

Distribution of the distances of the data to the best‐fit cylinder:

Scope  (13)

Data  (4)

RegionFit works on coordinates:

List of points:

Collections of points:

Oriented collections of points:

Models  (7)

Obtain an InfiniteLine that best fits a set of points:

Circle:

InfiniteLine in 3D:

Hyperplane:

Sphere:

Cylinder:

Cone:

Properties  (2)

RegionFit gives the best fit region:

Distances of each point from the best fit region:

Variance of the distances:

Inliers and outliers:

Options  (4)

Tolerance  (1)

Use Tolerance to control the maximum distance of inliers:

WorkingPrecision  (3)

Compute the best-fit model using machine arithmetic:

Find the fit using exact numbers:

Find the fit using 30 digits of precision:

Applications  (3)

Find a best-fit parametrized region for a set of points on a circle:

Show the exact fit:

A set of points with noise:

Find a best-fit parametrized region:

Visualize the fitted region with the data:

Find the equation of a line passing through a set of points:

Properties & Relations  (1)

For near-perfect linear data, RegionFit and Fit produce equivalent fits using LeastSquares:

Use Fit to find the equation of the line:

Use RegionFit to find the line region:

Compare the results:

Fit minimizes the least squares error across all points, while RegionFit ignores outliers:

Fit the data with an outlier:

Show the new fits:

Wolfram Research (2021), RegionFit, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionFit.html.

Text

Wolfram Research (2021), RegionFit, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionFit.html.

CMS

Wolfram Language. 2021. "RegionFit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RegionFit.html.

APA

Wolfram Language. (2021). RegionFit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionFit.html

BibTeX

@misc{reference.wolfram_2024_regionfit, author="Wolfram Research", title="{RegionFit}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/RegionFit.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_regionfit, organization={Wolfram Research}, title={RegionFit}, year={2021}, url={https://reference.wolfram.com/language/ref/RegionFit.html}, note=[Accessed: 21-November-2024 ]}