Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

Wolfram Language & System Documentation Center

EulerCharacteristic

EulerCharacteristic

EulerCharacteristic[poly]

gives the Euler characteristic of a poly.

Details

EulerCharacteristic is also known as Euler number or Euler–Poincaré characteristic.
EulerCharacteristic is a topological invariant that describes the shape of the polyhedron, regardless of the way it is bent.
The Euler characteristic 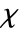for a polyhedron is given by , where 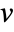is the number of vertices, 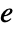the number of edges and 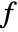the number of faces.
A polyhedron with 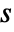voids and 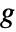tunnels satisfies .
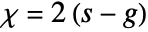The Euler characteristic for a mesh region is given by χ=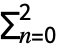(-1)ⁿMeshCellCount[poly,n].

Examples

open all close all

Basic Examples (1)

Euler characteristic of a polyhedron:

Scope (4)

EulerCharacteristic works on polyhedrons:

Polyhedron with holes:

Polyhedrons with disconnected components:

EulerCharacteristic works on mesh regions:

Properties & Relations (3)

Use EulerCharacteristic to compute PolyhedronGenus for a simple polyhedron:

Euler characteristic of a convex polyhedron equals 2:

Euler characteristic of UniformPolyhedron is 2:

Top