ExponentialMovingAverage
ExponentialMovingAverage[list,α]
给出 list 的指数移动平均数,带有平滑常数 α.
更多信息
- 平滑常数 α 通常是一个介于 0 和 1 之间的数,可以是任意表达式.
- ExponentialMovingAverage[x,α] 生成一个结果
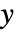 的列表,其中
的列表,其中 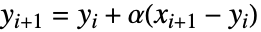 . »
. » - ExponentialMovingAverage[list,α] 的输出具有与 list 相同的长度.
- ExponentialMovingAverage 处理数值和符号数据.
- ExponentialMovingAverage 可以和 SparseArray 和 TemporalData 对象连用. »
范例
打开所有单元关闭所有单元推广和延伸 (2)
Wolfram Research (2007),ExponentialMovingAverage,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ExponentialMovingAverage.html.
文本
Wolfram Research (2007),ExponentialMovingAverage,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ExponentialMovingAverage.html.
CMS
Wolfram 语言. 2007. "ExponentialMovingAverage." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ExponentialMovingAverage.html.
APA
Wolfram 语言. (2007). ExponentialMovingAverage. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ExponentialMovingAverage.html 年