FindGraphIsomorphism

FindGraphIsomorphism[g1,g2]

通过重命名顶点找到将图 g1 映射到 g2 的同构.

FindGraphIsomorphism[g1,g2,n]

找到至多 n 个同构.

FindGraphIsomorphism[{vw,…},…]

使用规则 vw 指定图 g.

更多信息和选项

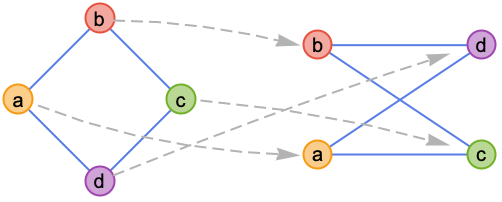
范例

打开所有单元关闭所有单元

基本范例  (2)

求映射两个图的同构：

求所有同构：

范围  (8)

规范  (5)

FindGraphIsomorphism 适用于无向图：

有向图：

使用规则指定图：

如果不能找到图同构，则返回空列表：

FindGraphIsomorphism 适用于大型图：

枚举  (3)

求映射两个图的同构：

求至多两个同构关系：

找到全部同构：

应用  (1)

求映射两个图的同构：

根据映射，突出显示和对两个图添加标签：

属性和关系  (3)

同构的图具有相同数目的顶点和边：

使用 IsomorphicGraphQ 检验两个图是否是同构的：

同构图具有相同的规范图：

Wolfram Research (2010)，FindGraphIsomorphism，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FindGraphIsomorphism.html （更新于 2015 年）.

文本

Wolfram Research (2010)，FindGraphIsomorphism，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FindGraphIsomorphism.html （更新于 2015 年）.

CMS

Wolfram 语言. 2010. "FindGraphIsomorphism." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/FindGraphIsomorphism.html.

APA

Wolfram 语言. (2010). FindGraphIsomorphism. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FindGraphIsomorphism.html 年

BibTeX

@misc{reference.wolfram_2024_findgraphisomorphism, author="Wolfram Research", title="{FindGraphIsomorphism}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/FindGraphIsomorphism.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_findgraphisomorphism, organization={Wolfram Research}, title={FindGraphIsomorphism}, year={2015}, url={https://reference.wolfram.com/language/ref/FindGraphIsomorphism.html}, note=[Accessed: 21-November-2024 ]}