FindShortestPath

FindShortestPath[g,s,t]

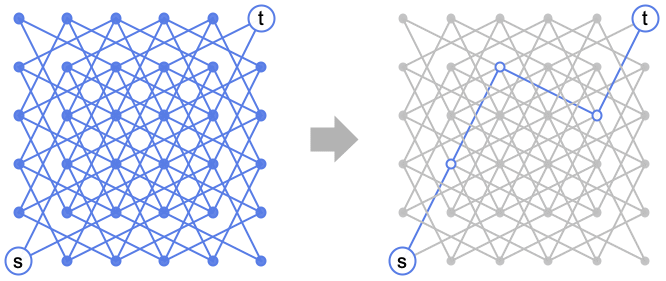
グラフ g 中のソース頂点 s からターゲット頂点 t までの最短経路を求める．

FindShortestPath[g,s,All]

異なる t に繰り返し適用できるShortestPathFunction[…]を生成する．

FindShortestPath[g,All,t]

異なる s に繰り返し適用できるShortestPathFunction[…]を生成する．

FindShortestPath[g,All,All]

異なる s と t に繰り返し適用できるShortestPathFunction[…]を生成する．

FindShortestPath[{vw,…},…]

規則 vw を使ってグラフ g を指定する．

詳細とオプション

  • FindShortestPath[g,s,t]は s から t までの経路を与える．
  • FindShortestPath[g,s]はFindShortestPath[g,s,All]に等しい．
  • FindShortestPath[g]はFindShortestPath[g,All,All]に等しい．
  • 重みなしのグラフの場合，辺の長さは1であるとみなされる．
  • 重み付きのグラフの場合，辺の長さはその重みであるとみなされる．
  • Methodを与えることもできる．次は使用可能なMethodの設定値である．
  • "BellmanFord"正負の重みをサポート
    "Dijkstra"正の重みをサポート
  • FindShortestPathは，無向グラフ，有向グラフ，重み付きグラフ，多重グラフ，混合グラフに用いることができる．

例題

すべて開くすべて閉じる

例  (1)

グラフ内の異なる2つの頂点間の最短経路を求める：

経路をハイライトする：

スコープ  (9)

指定  (7)

FindShortestPathは無向グラフに使うことができる：

有向グラフ：

多重グラフ：

混合グラフ：

重み付きのグラフ：

最短経路は辺重みの合計が最小である：

規則を使ってグラフを指定する：

大きいグラフに使うことができる：

コレクション  (2)

ある頂点から他のすべての頂点への最短経路を求める：

ShortestPathFunctionをグラフのすべての頂点に適用する：

すべての頂点からある一つの頂点への最短経路を求める：

ShortestPathFunctionをグラフのすべての頂点に適用する：

オプション  (3)

Method  (3)

メソッドは入力によって自動的に選ばれる：

"UnitWeight"メソッドはすべての辺に重み1を使う：

"Dijkstra"は辺の重みが正のグラフのみに使うことができる：

アプリケーション  (3)

木の最短経路を求める：

サッカーボールの縫い目に沿って最短経路を求める：

格子グラフのランダムな深さ優先探索で迷路を作る：

迷路を解く：

特性と関係  (1)

2つの頂点間の距離は最短経路を使って求めることができる：

Wolfram Research (2010), FindShortestPath, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindShortestPath.html （2015年に更新）.

テキスト

Wolfram Research (2010), FindShortestPath, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindShortestPath.html （2015年に更新）.

CMS

Wolfram Language. 2010. "FindShortestPath." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/FindShortestPath.html.

APA

Wolfram Language. (2010). FindShortestPath. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindShortestPath.html

BibTeX

@misc{reference.wolfram_2024_findshortestpath, author="Wolfram Research", title="{FindShortestPath}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/FindShortestPath.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_findshortestpath, organization={Wolfram Research}, title={FindShortestPath}, year={2015}, url={https://reference.wolfram.com/language/ref/FindShortestPath.html}, note=[Accessed: 21-November-2024 ]}