gives the matrix of distances between vertices for the graph g.
GraphDistanceMatrix[g,d]
gives the matrix of distances between vertices of maximal distance d in the graph g.
GraphDistanceMatrix[{vw,…},…]
uses rules vw to specify the graph g.


GraphDistanceMatrix
gives the matrix of distances between vertices for the graph g.
GraphDistanceMatrix[g,d]
gives the matrix of distances between vertices of maximal distance d in the graph g.
GraphDistanceMatrix[{vw,…},…]
uses rules vw to specify the graph g.
Details and Options

- GraphDistanceMatrix is also known as the shortest path matrix.
- GraphDistanceMatrix returns a SparseArray object or an ordinary matrix.
- The entries of the distance matrix dij give the shortest distance from vertex vi to vertex vj.
- The diagonal entries dii of the distance matrix are always zero.
- The entry dij is Infinity (∞) if there is no path from vertex vi to vertex vj.
- In GraphDistanceMatrix[g,d], an entry dij will be Infinity if there is no path from vertex vi to vertex vj in d steps or less.
- The vertices vi are assumed to be in the order given by VertexList[g].
- For a weighted graph, the distance is the minimum of the sum of weights along any path from vertex vi to vertex vj.
- The following options can be given:
-
EdgeWeight Automatic weight for each edge Method Automatic method to use - Possible Method settings include "Dijkstra", "FloydWarshall", and "Johnson".
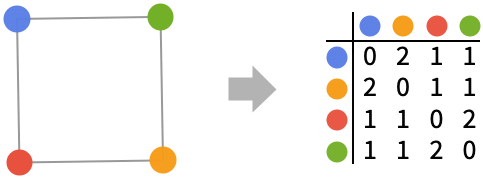
Examples
open all close allScope (8)
GraphDistanceMatrix works with undirected graphs:
Use rules to specify the graph:
Extract a single matrix column for a graph of modest size:
Using GraphDistance to compute the same result takes more time:
GraphDistanceMatrix works with large graphs:
When just a single column is needed and the graph is large, using GraphDistance is faster:
Options (6)
Method (6)
The method is automatically chosen depending on input:
"UnitWeight" method will use the weight 1 for every edge:
"Dijkstra" can be used for graphs with positive edge weights only:
"FloydWarshall" can be used for directed graphs including negative edge weights:
"Johnson" can be used for directed graphs including negative edge weights:
"Johnson" can be faster than the "FloydWarshall" method on sparse graphs:
Applications (2)
Find the vertex eccentricity, taking the entire graph into account:
For the strongly connected graph, the result is in agreement with VertexEccentricity:
Find the vertex eccentricity of every vertex in a connected graph:
Properties & Relations (5)
Rows and columns of the distance matrix follow the order given by VertexList:
The diagonal entries of the distance matrix are always zero:
The distance matrix can be found using GraphDistance:
In a connected graph, the VertexEccentricity can be obtained from the distance matrix:
The distance between two vertices belonging to different connected components is Infinity:
Possible Issues (2)
The matrix indices may not have the expected correspondence to vertices:
The distance from 2 to 3 is not at the expected matrix position:
The reason is that vertices are not in the expected order:
Solve the problem by listing vertices explicitly when calling functions such as Graph:
Now the distance is found at the expected position:
"BellmanFord" is not a valid Method option:
Use "FloydWarshall", "Johnson", or the default choice of Method instead:
Neat Examples (1)
Related Guides
Text
Wolfram Research (2010), GraphDistanceMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html (updated 2015).
CMS
Wolfram Language. 2010. "GraphDistanceMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html.
APA
Wolfram Language. (2010). GraphDistanceMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html
BibTeX
@misc{reference.wolfram_2025_graphdistancematrix, author="Wolfram Research", title="{GraphDistanceMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html}", note=[Accessed: 06-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_graphdistancematrix, organization={Wolfram Research}, title={GraphDistanceMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html}, note=[Accessed: 06-January-2026]}