WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

FindTreeGameStrategies[tgame]

TreeGame tgame に対する最適戦略プロファイルを求める．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
アプリケーション  
社会ゲーム  
娯楽ゲーム  
歴史的なゲーム  
おもしろい例題  
関連項目
関連するガイド
履歴
引用書式

FindTreeGameStrategies

FindTreeGameStrategies[tgame]

TreeGame tgame に対する最適戦略プロファイルを求める．

詳細とオプション

  • FindTreeGameStrategiesは，部分ゲーム完全均衡としても知られている．
  • 木ゲームの戦略プロファイルは，指定された任意の行動ノードにおける任意のプレーヤーの動作を指定する確率分布の集合である．
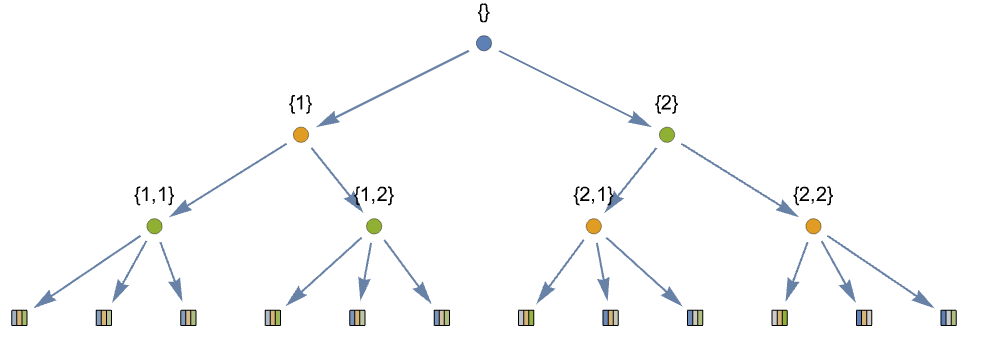
  • 任意の行動ノードを指定するためには，それに達するために選択リスト，例えば，最初の行動を取るための{1}，2番目の行動を取って次に最初の行動を取るための{2,1}，最初の（ルート）行動ノード{}を使う．
  • 部分ゲーム完全均衡は，一つの行動の確率分布を変えただけではどのプレーヤーも自分の利得が改善できない木ゲーム戦略プロファイルとして定義される．
  • FindTreeGameStrategiesはTreeGameについてゲームの全プレーヤーにとって互いに最適な戦略集合を見付けようとする．
  • 木ゲーム戦略プロファイル<|…,playeri<|ni,1pri,1,…,ni,mipri,mi|>,…|>は，playeriの行動ノード ni,jの playeriの行動確率 pri,jを指定する．
  • 例えば，戦略<|"A" <|{} {0.7, 0.3}|>, "B" <|{2} {0.4, 0.6}|>|> <|"A" <|{} {0.7, 0.3}|>, "B" <|{2} {0.4, 0.6}|>|>は「プレーヤー"A"の最初の選択のおよびプレーヤー"B"の2番目の選択がより高い確率」のように表現されるだろう．

例題

すべて開く すべて閉じる

例  (4)

硬貨合せゲームの木ゲームの最適戦略を求める：

Wolfram Language code: FindTreeGameStrategies[GameTheoryData["TreeMatchingPennies"]]

革命ゲームの最適戦略を求める：

Wolfram Language code: FindTreeGameStrategies[GameTheoryData["Revolution"]]

戦略を可視化する：

Wolfram Language code: TreeGamePlot[GameTheoryData["Revolution"], %[[1]]]

エスカレーションゲームの最適戦略を求める：

Wolfram Language code: FindTreeGameStrategies[GameTheoryData["Escalation"]]

エスカレーションゲームの最初の行動は確率に基づいているので，戦略は各選択について検討される：

Wolfram Language code: TreeGamePlot[GameTheoryData["Escalation"], <|"Nature" -> <||>, "A" -> <|{1} -> {0, 1}, {2} -> {1, 0}|>, "B" -> <|{1, 2} -> {1, 0}, {2, 2} -> {0, 1}|>|>]

TreeGameを生成する：

Wolfram Language code: game = TreeGame[{"A", {"B", {"C", {1, 2, 3}, {3, 2, 1}, {3, 1, 2}}, {"C", {0, 2, 4}, {4, 2, 0}, {4, 0, 2}}}, {"C", {"B", {-1, 2, 5}, {5, 2, -1}, {5, -1, 2}}, {"B", {-2, 2, 6}, {6, 2, -2}, {6, -2, 2}}}}]

部分ゲーム完全均衡をすべて求める：

Wolfram Language code: FindTreeGameStrategies[game]

これは，グラフにした方がはるかに簡単に可視化できる：

Wolfram Language code: TreeGamePlot[game, FindTreeGameStrategies[game][[1]]]

スコープ  (3)

参入ゲームの最適戦略を求める：

Wolfram Language code: FindTreeGameStrategies[GameTheoryData["Entry"]]

最後通牒ゲームについて考える：

Wolfram Language code: ultimatum = TreeGame[{1, {2, {0, 0} -> "No", {2, 0} -> "Yes"} -> "A", {2, {0, 0} -> "No", {1, 1} -> "Yes"} -> "B", {2, {0, 0} -> "No", {0, 2} -> "Yes"} -> "C"}];

このゲームの最適戦略を求める：

Wolfram Language code: FindTreeGameStrategies[ultimatum]

これがどの行動に対応するのかを判定する：

Wolfram Language code: TreeGamePlot[ultimatum, %[[1]]]

硬貨合せゲームの逐次形式における最適戦略を求める：

Wolfram Language code: FindTreeGameStrategies[GameTheoryData["TreeMatchingPennies"]]

アプリケーション  (6)

社会ゲーム  (2)

ムカデゲームのプレーヤーは2人で，この2人が交互に決定を下す．各手番でプレーヤーは「下に」降りてゲームを終らせるか「横」に進んでゲームを続けるかすることができる（最終ノードは例外で「横」に進んでもゲームは終る）．ゲームが長く続くほど合計利得は高くなる．しかし，先にゲームを終ったプレーヤーがより高い利得を得る．次は，問題の一つの定式化である：

Wolfram Language code: GameTheoryData["Centipede", "Description"]
Wolfram Language code: game = GameTheoryData["Centipede"]

このゲームの最適戦略を求める：

Wolfram Language code: FindTreeGameStrategies[game]

ゲームの解の木からも分かるように，ゲーム理論的に見ると，どの段階でも最善の解決策はゲームを早期に終了することである：

Wolfram Language code: TreeGamePlot[game, %[[1]]]

硬貨合せゲームの木ゲームは2人のプレーヤーのそれぞれが表か裏を選ぶゲームである．選択したものが異なる場合はプレーヤー1がプレーヤー2に1ドル支払い，選択したものが同じならプレーヤー2がプレーヤー1に1ドル支払う．硬貨合せゲームの木ゲームを生成する：

Wolfram Language code: game = GameTheoryData["TreeMatchingPennies"]

このゲームの最適ゲーム戦略を求める：

Wolfram Language code: FindTreeGameStrategies[game]

このゲームの逐次的性質のため，プレーヤー2にはプレーヤー1の選択に基づいて最良の結果を選ぶことができるというアドバンテージがある．結果として，{-1,1}の利得が保証されているので，プレーヤー1が何を選ぶかは問題ではない：

Wolfram Language code: TreeGamePlot[game, %[[1]]]

娯楽ゲーム  (2)

ジャンケンは，一人のプレーヤーが勝って他が負けるか引き分けるかのゼロ和ゲームである．プレーヤ2がプレーヤ1の選択を考慮して行動を選択できる，このゲームの木バージョンを生成する：

Wolfram Language code: game = TreeGame[{"A", {"B", {0, 0} -> "Rock", {-1, 1} -> "Paper", {1, -1} -> "Scissors"} -> "Rock", {"B", {1, -1} -> "Rock", {0, 0} -> "Paper", {-1, 1} -> "Scissors"} -> "Paper", {"B", {-1, 1} -> "Rock", {1, -1} -> "Paper", {0, 0} -> "Scissors"} -> "Scissors"}]

明らかに，ジャンケンの木ゲームの場合は，プレーヤー2が常に最適行動を選択でき，したがって，プレーヤー1は先にプレーすることで不利益を被る．このゲームの最適戦略を求める：

Wolfram Language code: FindTreeGameStrategies[game]

3x3の行列を使った3目並べのゲームを検討する．1は"X"を，は"O"を，0は空白スペースを表す：

Wolfram Language code: ticTacToeTree[game_, player_] := If[StringContainsQ[ToString[Total /@ Join[game, Transpose[game], {Diagonal[game]}, {game[[1, 3]], game[[2, 2]], game[[3, 1]]}]], "3"], If[player == "A", {-1, 1}, {1, -1}], If[!MemberQ[Flatten[game], 0], {0, 0}, Prepend[Flatten[Table[Module[{g = game}, If[game[[i, j]] == 0, g[[i, j]] = If[player == "A", 1, -1]; ticTacToeTree[g, If[player == "A", "B", "A"]] -> ToString[{i, j}], Nothing] ], {i, 3}, {j, 3}], 1], player] ] ]

3目並べの部分的に完了したゲームについて考える：

Wolfram Language code: map = (⁠| | | | | - | - | -- | | 1 | 0 | -1 | | 0 | 1 | 0 | | 1 | 0 | -1 |⁠);

上記に基づいてTreeGameを形成する：

Wolfram Language code: game = TreeGame[ticTacToeTree[map, "B"]]

最適戦略を可視化する：

Wolfram Language code: TreeGamePlot[game, FindTreeGameStrategies[game][[1]]]

歴史的なゲーム  (2)

革命ゲームは次のようなものである．植民地には現状に抵抗するかこれを認めるかの選択肢がある．支配国は独立を認めるか抵抗を鎮圧するかできる．植民地が現状を認めた場合，支配国は課税することもしないこともできる．このゲームは，通常，抵抗が鎮圧された場合の利得が不明の状態で研究される．ゲームを可視化する：

Wolfram Language code: game = TreeGamePlot[GameTheoryData["Revolution"]]

ゲームを解く：

Wolfram Language code: FindTreeGameStrategies[GameTheoryData["Revolution"]]

海軍配置ゲームはビスマルクの戦いゲームを敗走する師団と追撃する師団に拡張したものである：

Wolfram Language code: game = TreeGame[{1, {0, 5}, {2 -> 1, {5, 0}, {-1, -2}}, {2 -> 1, {5, 0}, {-3, -5}}}]

部分ゲーム完全均衡を求める：

Wolfram Language code: FindTreeGameStrategies[game]

おもしろい例題  (1)

Rainbow Warshipゲームには石油会社（プレーヤー1）と環境活動家（プレーヤー2）の2人のプレーヤーがいる．石油会社には3つの小さく連続した領域を移動可能な単一の石油採掘プラットフォームがある．海底の各エリアには異なる量の原油が埋蔵されており，毎晩違法にこれを採掘することができる．環境活動家は，違法採掘を証明してゲームを終了するために，石油会社のこの採掘行為を現行犯で捕まえなければならない．彼らは1つの領域しかカバーできない送信機を1日に1つしか打ち上げることができない．3つのセル（左，真ん中，右）のRainbow Warshipゲームを入力する：

Wolfram Language code: game = TreeGame[{1, {2 -> 1, {0, 0} -> "Left", {2 -> 2, {1, -1} -> "Left", {2, -2} -> "Right"} -> "Middle", {1, {2 -> 5, {1, -1} -> "Left", {2, -2} -> "Middle"} -> "Left", {2 -> 5, {3, -3} -> "Left", {1, -1} -> "Middle"} -> "Middle"} -> "Right"} -> "Left", {2 -> 1, {1, {2 -> 3, {2, -2} -> "Middle", {4, -4} -> "Right"} -> "Middle", {2 -> 3, {5, -5} -> "Middle", {2, -2} -> "Right"} -> "Right"} -> "Left", {0, 0} -> "Left", {1, {2 -> 4, {2, -2} -> "Left", {3, -3} -> "Middle"} -> "Left", {2 -> 4, {4, -4} -> "Left", {2, -2} -> "Middle"} -> "Middle"} -> "Right"} -> "Middle", {2 -> 1, {1, {2 -> 6, {3, -3} -> "Middle", {2, -2} -> "Right"} -> "Middle", {2 -> 6, {6, -6} -> "Middle", {3, -3} -> "Right"} -> "Right"} -> "Left", {2 -> 2, {6, -6} -> "Left", {3, -3} -> "Right"} -> "Middle", {0, 0} -> "Right"} -> "Right"}]

TreeGamePlotを使ってゲームを可視化する：

Wolfram Language code: TreeGamePlot[game]

情報集合を無視して，このゲームの最適戦略を求める：

Wolfram Language code: FindTreeGameStrategies[game]

TreeGamePlotオプションを使うとより簡単に可視化できる：

Wolfram Language code: TreeGamePlot[game, %[[1]]]
Wolfram Research (2025), FindTreeGameStrategies, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindTreeGameStrategies.html.

テキスト

Wolfram Research (2025), FindTreeGameStrategies, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindTreeGameStrategies.html.

CMS

Wolfram Language. 2025. "FindTreeGameStrategies." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FindTreeGameStrategies.html.

APA

Wolfram Language. (2025). FindTreeGameStrategies. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindTreeGameStrategies.html

BibTeX

@misc{reference.wolfram_2026_findtreegamestrategies, author="Wolfram Research", title="{FindTreeGameStrategies}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/FindTreeGameStrategies.html}", note=[Accessed: 03-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_findtreegamestrategies, organization={Wolfram Research}, title={FindTreeGameStrategies}, year={2025}, url={https://reference.wolfram.com/language/ref/FindTreeGameStrategies.html}, note=[Accessed: 03-November-2026]}