-
関連項目
- 関数
- FiniteGroupCount
- FiniteAbelianGroupCount
- GraphData
- LatticeData
-
- 実体タイプ
- FiniteGroup
-
- インタープリタタイプ
- FiniteGroup
- ComputedFiniteGroup
- 関連するガイド
-
-
関連項目
- 関数
- FiniteGroupCount
- FiniteAbelianGroupCount
- GraphData
- LatticeData
-
- 実体タイプ
- FiniteGroup
-
- インタープリタタイプ
- FiniteGroup
- ComputedFiniteGroup
- 関連するガイド
-
関連項目
FiniteGroupData[name,"property"]
name で指定された有限群の指定特性の値を返す.
FiniteGroupData["class"]
指定した類の有限群のリストを返す.


FiniteGroupData
FiniteGroupData[name,"property"]
name で指定された有限群の指定特性の値を返す.
FiniteGroupData["class"]
指定した類の有限群のリストを返す.
詳細












- 群に指定には "C3","Quaternion",{"SymmetricGroup",4}のような一般的な名称が使える.
- FiniteGroupData[name]は name で指定される群の名前の標準的な形を返す.
- FiniteGroupData[patt]は,文字列パターン patt にマッチするすべての群の名前を返す.
- FiniteGroupData[]およびFiniteGroupData[All]は,"Quaternion"のような使用可能な名前付き有限群および{"SymmetricGroup",deg}の最初の10族のように少数の無限族を返す.FiniteGroupDataはこれらの無限族の他の族にも使うことができる.
- FiniteGroupData[{n, id},…]は識別子 id を持つ位数 n の有限群のデータを返す.
- FiniteGroupData[n]は位数 n の使用可能な非同型有限群のリストを返す.
- FiniteGroupData[;;n]は位数 n までの非同型群のリストを返す.
- FiniteGroupData[n1;;n2]は位数 n1から位数 n2までの非同型有限群のリストを返す.
- FiniteGroupData[{"type", id}, …]は識別子が id である指定タイプの有限群のデータを返す.識別子は一般に整数かあるいは整数のリストである.
- 次は,基本的な群の族である.
-
{"AlternatingGroup",n} 代替群 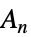
{"CrystallographicPointGroup",n} 三次元結晶点群 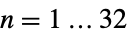
{"CyclicGroup",n} 巡回群 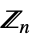
{"CyclicGroupUnits",n} 巡回群中の単位群 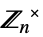
{"DicyclicGroup",n} 非巡回群 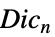
{"DihedralGroup",n} 二面体群 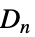
{"PointGroup",id} 三次元点群 {"SymmetricGroup",n} 対称群 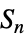
- 次は,有限単純群である.
-
{"ProjectiveSpecialLinearGroup",{n,q}} 射影特殊線形群 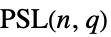
{"ProjectiveSymplecticGroup",{n,q}} 射影斜交群 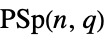
{"ChevalleyGroupB",{n,q}} 例外的なシュヴァレー(Chevalley)群 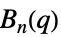
{"ChevalleyGroupD",{n,q}} 例外的なシュヴァレー群 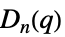
{"ChevalleyGroupE",{n,q}} 例外的なシュヴァレー群 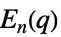 ,
, 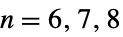
{"ChevalleyGroupF",{4,q}} 例外的なシュヴァレー群 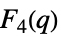
{"ChevalleyGroupG",{2,q}} 例外的なシュヴァレー群 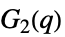
{"ReeGroupF",q} リー(Ree)群 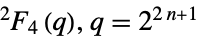
{"ReeGroupG",q} リー群 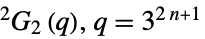
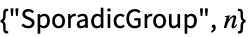
散在群 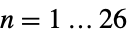
{"SteinbergGroupA",{n,q}} スタインバーグ(Steinberg)のユニタリ群 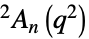
{"SteinbergGroupD",{n,q}} スタインバーグの直交群 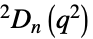
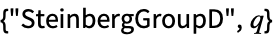
スタインバーグの直交群 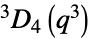
{"SteinbergGroupE",q} スタインバーグの直交群 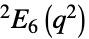

鈴木群 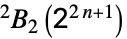
- 特殊な群指定
-
{"AbelianGroup",{m,n,…}} アーベル群 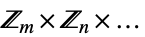
{"DirectProduct",{group1,group2,…}} 群の直積 {"SemiDirectProduct",{group1,…}} 群の半直積 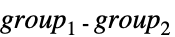 ,
, 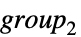 は結果では標準的である
は結果では標準的である - FiniteGroupData["Properties"]は群の使用可能な特性リストを返す.
- 基本的な群の特性
-
"Center" 群の中心(可換元) "CenterElements" 中心部分群の元 "ClassNumber" 類の数 "CommutatorSubgroup" 交換子群 "CommutatorSubgroupElements" 交換子群の元 "ConjugacyClasses" 共役類 "ElementNames" 元の名前のリスト "Elements" 群の元 "Exponent" 群の指数 "Generators" 生成元 "InverseGenerators" 生成元の逆元 "Inverses" 逆元 "MultiplicationTable" 掛け算表 "NormalSubgroupElements" 正規部分群の元 "NormalSubgroups" 正規部分群 "Order" 元の総数 "SubgroupElements" 部分群の元 "Subgroups" 部分群 "SylowSubgroupCounts" シロウ(Sylow)部分群のサイズ "SylowSubgroupElements" シロウ部分群の元 "SylowSubgroups" 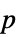 シロウ部分群
シロウ部分群 - 群の元は1からその群の位数までの整数で指定される.1は単位元に相当する.
- 群構造特性
-
"AutomorphismGroup" 自己同型群 "InnerAutomorphismGroup" 内部自己同型群 "IsomorphicGroups" 同型群のリスト "OuterAutomorphismGroup" 外部自己同型群 "QuotientGroups" 商群のリスト "SchurMultiplier" シューア乗数 - 置換群特性
-
"CycleIndex" 巡回指数 "Cycles" 巡回 "PermutationRepresentation" 置換リストとしての表現 "PermutationGroupRepresentation" Wolframシステムの置換群としての表現 "Transitivity" 移行性レベル - その他の特性
-
"DefiningRelations" 群多元環を説明する関係 "CayleyGraph" 組込みの方法で生成器を選んだケーリー(Cayley)グラフ "Classes" 群が属す類 "CycleGraph" 巡回グラフ "Information" 群についての情報 "ParameterRange" パラメータについての仮定 - 群表現特性
-
"CharacterTable" 群の元の指標 "ConjugacyClassNames" 共役類の名前 "ConjugacyClassSizes" 共役類のサイズ "MatrixRepresentation" 行列としての表現 "RepresentationDimensions" 表現の次元 "RepresentationNames" 表現の名前 "SpaceRepresentation" 3D直交座標変換としての表現 - 結晶点群のその他の特性
-
"BravaisLattices" 互換ブラべ(Bravais)格子 "CrystalForm" 結晶形 "CrystalSystem" 結晶系 "HermannMauguin" へルマン・モーガン(Hermann–Mauguin)表記 "Orbifold" オービフォルド記法 "PointGroupType" 点群のタイプ "Schoenflies" シェーンフリース(Schoenflies)表記 "Shubnikov" シューブニコフ(Shubnikov)表記 - FiniteGroupData["Classes"]はサポートされているすべての類のリストを返す.
- FiniteGroupData[name,"Classes"]は指定された群が含まれるすべての類のリストを返す.
- FiniteGroupData[name,"class"]は name に対応する群が指定の類にあるかどうかによってTrueまたはFalseを返す.
- FiniteGroupData["class"]はFiniteGroupData[]中の指定の類に属する有限群のリストを返す.
- FiniteGroupData["class",n]は指定の類中の n 位数の有限群のリストを返す.
- FiniteGroupData["class",;;n]は指定された類中の位数が n 以下の有限群のリストを返す.
- FiniteGroupData["class",n;;]は指定した類の中で位数が n 以上の標準有限群のリストを返す.
- FiniteGroupData["class",n1;;n2]は指定した類の中で位数が n1より大きいか n2より小さいすべての標準有限群のリストを返す.
- 群の類
-
"Abelian" 可換(アーベル) "Alternating" 交代 "Cyclic" 巡回 "Dihedral" 二面 "Perfect" 完全 "Simple" 単純 "Solvable" 可解 "Sporadic" 散在 "Symmetric" 対称 "Transitive" 移行 - 群の負の類
-
"Nonabelian" 非可換 "Nonalternating" 非交代 "Noncyclic" 非巡回 "Nondihedral" 非二面 "Nonperfect" 非完全 "Nonsimple" 非単純 "Nonsolvable" 非可解 "Nonsporadic" 非散在 "Nonsymmetric" 非対称 "Nontransitive" 非変換 - 群は,それぞれ同じ次数の交代群,巡回群,二面群または対称群と同型である場合は,"Alternating","Cyclic","Dihedral","Symmetric"のいずれかの類に属す.
- 群は,与えらえた対応する置換表現が推移的である場合は"Transitive"類に属す.{"DirectProduct",{group1,group2,…}}の置換表現は,商群のそれぞれの群作用の領域の互いに素な結合で構築されるため推移的ではない.
- 命名関連特性
-
"AlternateNames" 代替的な英語名を文字列で "AlternateStandardNames" 代替的な標準Wolfram言語名 "Name" 英語名を文字列で "Notation" 群の表記 "ShortName" 短縮名を文字列で "StandardName" 標準Wolfram言語名 - FiniteGroupData[name,"Information"]は指定された群の追加情報へのハイパーリンクを返す.
- FiniteGroupDataの使用にはインターネットの接続が必要なことがある.
例題
すべて開く すべて閉じるスコープ (34)
名前と類 (6)
すべての名前付き有限群と無限族の成員若干.その多くが互いに同型である:
指定された類に属するFiniteGroupData[]中の群のリスト:
類の成員を指定の位数のものに制限する.これらはすべて互いに同型群である:
FiniteGroupData[n]は位数 n の非同型群のリストを,最初はアーベル群,次に
非アーベル群で返す:
FiniteGroupDataが与えられた群の名前付きバージョンを持たない場合,その群は{order,index}で指定される:
特性値 (3)
特性の詳細 (21)
名前と表記 (3)
基本的な群の特性 (4)
群表現 (4)
一般化と拡張 (2)
特性の中には群の無限族の記号パラメータについてのものもある:
しかし,このようなパラメータについてはほとんどの特性値は整数でなければならない.そのような場合にはMissing["NotApplicable"]が返される:
特性と関係 (3)
FiniteGroupCount[n]は位数 n の有限群の数を返す:
したがって,位数によって呼ばれると,FiniteGroupDataは非同型群のリストを返す:
FiniteAbelianGroupCount[n]は位数 n のアーベル群の数を返す:
n を法とした整数環の単元の群は常にアーベル群である.しかし,常に巡回群であるわけではない:
ある群の元に群の位数と同じ位数のものがあれば,その群は巡回群である.{"CyclicGroupUnits", n}の位数はEulerPhi[n]であり,CarmichaelLambda[n]はその元の中の最高の位数を返す:
例えば,次の群は,元の中に位数が群の位数と等しいものがあるので,巡回群である:
条件EulerPhi[n]CarmichaelLambda[n]は,2, 4, pk, 2pkの形で素数p≠2かつ k≥1の正の整数 n についてのみ守られる:
考えられる問題 (1)
関連項目
FiniteGroupCount FiniteAbelianGroupCount GraphData LatticeData
実体タイプ: FiniteGroup
インタープリタタイプ: FiniteGroup ComputedFiniteGroup
関連リンク
テキスト
Wolfram Research (2008), FiniteGroupData, Wolfram言語関数, https://reference.wolfram.com/language/ref/FiniteGroupData.html (2020年に更新).
CMS
Wolfram Language. 2008. "FiniteGroupData." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/FiniteGroupData.html.
APA
Wolfram Language. (2008). FiniteGroupData. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FiniteGroupData.html
BibTeX
@misc{reference.wolfram_2025_finitegroupdata, author="Wolfram Research", title="{FiniteGroupData}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/FiniteGroupData.html}", note=[Accessed: 30-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_finitegroupdata, organization={Wolfram Research}, title={FiniteGroupData}, year={2020}, url={https://reference.wolfram.com/language/ref/FiniteGroupData.html}, note=[Accessed: 30-December-2025]}