FromContinuedFraction[list]
reconstructs a number from the list of its continued fraction terms.


FromContinuedFraction
FromContinuedFraction[list]
reconstructs a number from the list of its continued fraction terms.
Details
- FromContinuedFraction[{a1,a2,a3,…}] returns
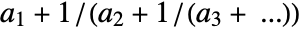 .
. - The ai can be symbolic. »
- FromContinuedFraction[{a1,a2,…,{b1,b2,…}}] returns the exact number whose continued fraction terms start with the ai, then consist of cyclic repetitions of the bi.
- FromContinuedFraction acts as the inverse of ContinuedFraction.
See Also
ContinuedFraction Convergents Rationalize ContinuedFractionK FromDigits Fold
Function Repository: FromNumberExpansion
Related Guides
History
Introduced in 1999 (4.0)
Text
Wolfram Research (1999), FromContinuedFraction, Wolfram Language function, https://reference.wolfram.com/language/ref/FromContinuedFraction.html.
CMS
Wolfram Language. 1999. "FromContinuedFraction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FromContinuedFraction.html.
APA
Wolfram Language. (1999). FromContinuedFraction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FromContinuedFraction.html
BibTeX
@misc{reference.wolfram_2025_fromcontinuedfraction, author="Wolfram Research", title="{FromContinuedFraction}", year="1999", howpublished="\url{https://reference.wolfram.com/language/ref/FromContinuedFraction.html}", note=[Accessed: 25-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_fromcontinuedfraction, organization={Wolfram Research}, title={FromContinuedFraction}, year={1999}, url={https://reference.wolfram.com/language/ref/FromContinuedFraction.html}, note=[Accessed: 25-January-2026]}