WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

FunctionDiscontinuities

FunctionDiscontinuities[f,x]

の x∈Realsについての不連続点を求める．

FunctionDiscontinuities[f,x,dom]

の x∈dom についての不連続点を求める．

FunctionDiscontinuities[{f₁,f₂,…},{x₁,x₂,…},dom]

の x₁,x₂,…∈dom についての不連続点を求める．

詳細

関数の不連続点は，関数の連続性が保証されている領域を求めるため，あるいは特別な解析が必要な点や線を求めるために使われることが多い．
FunctionDiscontinuitiesは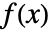，が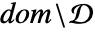で連続的となるような集合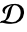の陰的な説明を与える．集合が最小である保証はない．
結果の陰的な説明は，ReduceやSolve等の関数での使用に適した，方程式，不等式，領域指定，これらの論理結合からなる．
dom の可能な値には，RealsとComplexesがある．

例題

すべて開くすべて閉じる

例 (4)

一変量実関数の不連続点を求める：

一変量複素関数の不連続点を求める：

多変量実関数の不連続点を求める：

多変量複素関数の不連続点を求める：

スコープ (5)

一変量実関数の不連続点：

からまでにある不連続点を求める：

不連続点を可視化する：

合成関数の不連続点：

からまでにある不連続点の有限集合を求める：

不連続点を可視化する：

実数上の不連続点には関数が実数値にはならない点も含まれる：

一変量複素関数の不連続点：

Re[z]とIm[z]について不連続点を計算する：

不連続点を可視化する：

多変量実関数の不連続点：

不連続点を可視化する：

アプリケーション (6)

基本的なアプリケーション (4)

の不連続性を求める：

からまでの不連続点を求める：

不連続性を可視化する：

の不連続性を求める：

不連続性がないことを示す：

関数は連続である：

複素関数の不連続性を求める：

Re[z]とIm[z]について不連続性を計算する：

不連続性を可視化する：

との不連続性が与えられた場合に，の不連続性を求める：

との不連続性がとの解集合に含まれていると仮定する：

の不連続性は解集合に含まれている：

微積分 (1)

がで連続なら $TemplateBox[{{f, (, x, )}, x, a}, Limit2Arg, DisplayFunction -> ({Sequence[{Sequence["lim"], _, DocumentationBuild`Utils`Private`Parenth[{#2, ->, #3}, LimitsPositioning -> True]}], #1} & ), InterpretationFunction -> ({Limit, [, {#1, ,, {#2, ->, #3}}, ]} & )]=f(a)$ である：

がで連続であることを確かめる：

におけるの極限は簡単な置換で求められる：

可視化 (1)

不連続性を使ってPlotのExclusions設定を求める：

不連続性をExclusionsが求める形式に変換する：

Plotにおける除外を使う：

除外を使わずに計算されたプロットと比較する：

特性と関係 (2)

関数は，FunctionDiscontinuitiesが与える集合の外では連続である：

FunctionContinuousを使って連続性をチェックする：

FunctionSingularitiesは，その外では関数が解析的になる集合を与える：

不連続点の集合は特異点の集合の部分集合である：

考えられる問題 (2)

返された不連続点集合は最小ではないかもしれない：

この関数は恒等的にゼロなので，不連続点がない：

不連続点の情報に欠けている部分があると，エラーメッセージが出て既知の不連続点が返される：

トップへ