WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

GraphAssortativity[g]w

頂点次数を使ってグラフ g の同類選択性係数を与える．

GraphAssortativity[g,"prop"]

頂点の特性"prop"を使ってグラフ g の同類選択性係数を与える．

GraphAssortativity[g,{{vi 1,vi 2,…},…}]

頂点分割{{vi 1,vi 2,…},…}についてのグラフ g の同類選択性係数を与える．

GraphAssortativity[g,{v1,v2,…}{x1,x2,…}]

頂点{v1,v2,…}についてデータ{x1,x2,…}を使ってグラフ g の同類選択性係数を与える．

GraphAssortativity[{vw,…},…]

規則 vw を使ってグラフ g を指定する．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
オプション  
"DataType"  
"Weighted"  
"Normalized"  
アプリケーション  
特性と関係  
関連項目
関連するガイド
履歴
引用書式

GraphAssortativity

GraphAssortativity[g]w

頂点次数を使ってグラフ g の同類選択性係数を与える．

GraphAssortativity[g,"prop"]

頂点の特性"prop"を使ってグラフ g の同類選択性係数を与える．

GraphAssortativity[g,{{vi 1,vi 2,…},…}]

頂点分割{{vi 1,vi 2,…},…}についてのグラフ g の同類選択性係数を与える．

GraphAssortativity[g,{v1,v2,…}{x1,x2,…}]

頂点{v1,v2,…}についてデータ{x1,x2,…}を使ってグラフ g の同類選択性係数を与える．

GraphAssortativity[{vw,…},…]

規則 vw を使ってグラフ g を指定する．

詳細とオプション

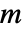  • 本の辺があり隣接行列の項が 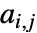であるグラフの場合，同類選択性係数は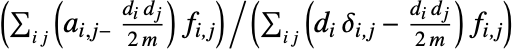で与えられる，ただし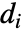， は頂点 viの出次数であり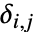， は viから vjまでの辺がある場合は1でその他の場合は0である．
  • x1,x2,…が使われている数量データの場合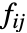， は xixjであると解釈される．
  • x1,x2,…が使われているカテゴリ的データの場合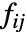，は xi と xj が等しい場合は1，それ以外の場合は0であると解釈される．
  • GraphAssortativity[g]では，xi は頂点 vi の頂点出次数であるとみなされる．
  • GraphAssortativity[g,"prop"]では，xi は頂点 vi についてAnnotationValue[{g,vi},"prop"]であるとみなされる．
  • GraphAssortativity[g,{{vi 1,vi 2,…},…}]では，部分集合{vi 1,vi 2,…}中の頂点は同じカテゴリ的データ xi 1=xi 2=…を持つものとみなされる．
  • GraphAssortativity[g,Automatic->{x1,x2,…}]は頂点リストがVertexList[g]であるとみなす．
  • GraphAssortativityは，以下のオプションを取る．
  • "DataType" Automaticデータ型
    "Normalized" True結果を正規化するかどうか
    "Weighted" Automatic辺の重み
  • オプション"DataType"->type を使ってデータ x1,x2,…のタイプを指定することができる．使用可能な設定値は"Quantitative"と"Categorical"である．
  • オプション"Normalized"->Falseを使って同類選択性モジュールを計算することができる．
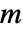  • 本の辺があり隣接行列の項が 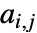であるグラフの場合，同類選択性モジュールは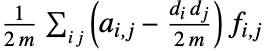で与えられる．ただし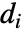， は頂点 viの出次数である，
  • GraphAssortativityは，無向グラフ，有向グラフ，重み付きグラフ，多重グラフ，混合グラフに使うことができる．

例題

すべて開く すべて閉じる

例  (2)

Zachary空手クラブのネットワークの同類選択性係数を計算する：

Wolfram Language code: GraphAssortativity[[image]]

一様ランダムグラフの同類選択性係数の分布：

Wolfram Language code: Histogram[Table[GraphAssortativity[RandomGraph[{100, 300}]], {2000}]]

スコープ  (12)

GraphAssortativityは無向グラフに使うことができる：

Wolfram Language code: GraphAssortativity[[image]]

有向グラフに使う：

Wolfram Language code: GraphAssortativity[[image]]

重み付きグラフに使う：

Wolfram Language code: GraphAssortativity[[image]]

多重グラフ：

Wolfram Language code: GraphAssortativity[[image]]

混合グラフ：

Wolfram Language code: GraphAssortativity[[image]]

規則を使ってグラフを指定する：

Wolfram Language code: GraphAssortativity[{1 -> 3, 2 -> 1, 3 -> 6, 4 -> 6, 1 -> 5, 5 -> 4, 6 -> 1}]

頂点の特性データを使って同類選択性係数を計算する：

Wolfram Language code: GraphAssortativity[[image], "VertexColor"]

頂点分割：

Wolfram Language code: GraphAssortativity[[image], {{1, 2, 7}, {3, 4}, {5, 6}}]

指定されたデータ集合：

Wolfram Language code: GraphAssortativity[[image], Range[7] -> RandomReal[1, 7]]

VertexListの部分集合の分割あるいは割当て：

Wolfram Language code: GraphAssortativity[[image], {{1, 2, 7}, {3, 4}}]

GraphAssortativityは記号式に使うことができる：

Wolfram Language code: GraphAssortativity[[image], Automatic -> {a, b, c, d}, "DataType" -> "Quantitative"]

GraphAssortativityは大きいグラフに使うことができる：

Wolfram Language code: g = ExampleData[{"NetworkGraph", "Internet"}];
Wolfram Language code: VertexCount[g]
Wolfram Language code: N[GraphAssortativity[g]]//Timing

オプション  (4)

"DataType"  (2)

"DataType"->"Quantitative"を使う：

Wolfram Language code: g = GridGraph[{2, 3}]
Wolfram Language code: data = {0.1, 0.1, 0.2, 0.2, 0.3, 0.3};
Wolfram Language code: GraphAssortativity[g, Automatic -> data]

データ型を指定する：

Wolfram Language code: GraphAssortativity[g, Automatic -> data, "DataType" -> "Quantitative"]

"DataType"->"Categorical"を使う：

Wolfram Language code: g = GridGraph[{2, 3}]
Wolfram Language code: data = {a, b, b, a, a, a};
Wolfram Language code: GraphAssortativity[g, Automatic -> data]

データ型を指定する：

Wolfram Language code: GraphAssortativity[g, Automatic -> data, "DataType" -> "Categorical"]

"Weighted"  (1)

デフォルトで，辺重みが使われる：

Wolfram Language code: g = [image];
Wolfram Language code: GraphAssortativity[g]

"Weighted"->Falseを使って辺重みを無視する：

Wolfram Language code: GraphAssortativity[g, "Weighted" -> False]

"Normalized"  (1)

デフォルトで，モジュール性の正規化された値が同類度係数として計算される：

Wolfram Language code: g = GridGraph[{2, 3}]
Wolfram Language code: GraphAssortativity[g]

"Normalized"->Falseを使って同類度モジュール性を計算する：

Wolfram Language code: GraphAssortativity[g, "Normalized" -> False]

アプリケーション  (3)

頂点の色による頂点分割の同類選択性係数を比較する：

Wolfram Language code: graphs = {[image], [image], [image], [image]};
Wolfram Language code: Labeled[#, GraphAssortativity[#, "VertexColor"]]& /@ graphs

友達ネットワーク中の友人数による非同類選択性：

Wolfram Language code: g = ExampleData[{"NetworkGraph", "ZacharyKarateClub"}];
Wolfram Language code: N[GraphAssortativity[g]]

ネットワーク中の分割は同類選択性を示す：

Wolfram Language code: partition = FindGraphPartition[g];
Wolfram Language code: HighlightGraph[g, Table[Subgraph[g, i], {i, partition}]]
Wolfram Language code: N[GraphAssortativity[g, partition]]

人種によって頂点に色を付けた高校の友達ネットワーク．生徒が同じ人種の生徒との付き合いを好む様子を分析する：

Wolfram Language code: g = \!\(\*GraphicsBox[«10»]\);

高度に社交的な生徒は他の高度に社交的な生徒と友達である：

Wolfram Language code: N[GraphAssortativity[g]]

同じ人種の生徒と付き合う傾向が強い：

Wolfram Language code: N[GraphAssortativity[g, "Race"]]

特性と関係  (2)

同類選択性係数は-1から1の間である：

Wolfram Language code: N[GraphAssortativity[RandomGraph[{100, 200}]]]

完全同類選択性グラフ：

Wolfram Language code: GraphAssortativity[GraphData[{5, 20}]]

完全非同類選択性グラフ：

Wolfram Language code: GraphAssortativity[StarGraph[5]]

GraphAssortativityは連結頂点間の次数のピアソン(Pearson)相関係数である：

Wolfram Language code: g = RandomGraph[{10, 20}];
Wolfram Language code: GraphAssortativity[g]

Correlationはピアソン相関係数を与える：

Wolfram Language code: x = EdgeList[g] /. i_j_ :> {VertexDegree[g, i], VertexDegree[g, j]};
Wolfram Language code: y = EdgeList[g] /. i_j_ :> {VertexDegree[g, j], VertexDegree[g, i]};
Wolfram Language code: Correlation[Flatten[x], Flatten[y]]
Wolfram Research (2012), GraphAssortativity, Wolfram言語関数， https://reference.wolfram.com/language/ref/GraphAssortativity.html （2015年に更新）.

テキスト

Wolfram Research (2012), GraphAssortativity, Wolfram言語関数， https://reference.wolfram.com/language/ref/GraphAssortativity.html （2015年に更新）.

CMS

Wolfram Language. 2012. "GraphAssortativity." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GraphAssortativity.html.

APA

Wolfram Language. (2012). GraphAssortativity. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphAssortativity.html

BibTeX

@misc{reference.wolfram_2026_graphassortativity, author="Wolfram Research", title="{GraphAssortativity}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GraphAssortativity.html}", note=[Accessed: 03-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_graphassortativity, organization={Wolfram Research}, title={GraphAssortativity}, year={2015}, url={https://reference.wolfram.com/language/ref/GraphAssortativity.html}, note=[Accessed: 03-November-2026]}