GraphDistance

GraphDistance[g,s,t]

グラフ g 上のソース頂点 s からターゲット頂点 t までの距離を返す．

GraphDistance[g,s]

グラフ g 上の頂点 s からすべての頂点までの距離を返す．

GraphDistance[{vw,…},…]

規則 vw を使ってグラフ g を指定する．

詳細とオプション

  • GraphDistanceは測地距離としても知られている．
  • GraphDistance[g,s,t] は s と t 間の最短経路の長さを与える．
  • s から t までの経路がない場合の距離はInfinityである．
  • 重み付きグラフの場合，距離は s から t までの任意の経路に沿った重みの総和の最小のものである．
  • 使用可能なオプション
  • Method Automatic使用するメソッド
  • Methodの可能な設定値には，"Dijkstra"，"BellmanFord"，"UnitWeight"がある．

例題

すべて開くすべて閉じる

例  (1)

格子グラフの距離を与える：

スコープ  (7)

GraphDistanceは無向グラフに使うことができる：

有向グラフ：

重み付きグラフ：

多重グラフ：

混合グラフ：

規則を使ってグラフを指定する：

GraphDistanceは大きいグラフに使うことができる：

オプション  (4)

Method  (4)

メソッドは入力に従って自動的に選ばれる：

"UnitWeight"メソッドはすべての辺に重み1を使う：

"Dijkstra"は辺の重みが正であるグラフにのみ使うことができる：

"BellmanFord"は，負の辺の重みを含む有向グラフに使うことができる：

アプリケーション  (5)

サイズ{6,6}のGridGraphの相対するコーナーの間の距離を求める：

次元のサイズが{6,6,…,6}のGridGraphの相対するコーナーの間の距離を求める：

木の頂点からの距離を可視化する：

ある頂点から他の任意の頂点までの最大距離を求める：

距離に比例するように色付けする：

確率 のベルヌーイ(Bernoulli)グラフの2頂点間の距離の期待値は である：

アルファベットを使った短い単語のDamerauLevenshteinDistanceを示す：

2つの単語のDamerau–Levenshtein距離を求める：

結果を確かめる：

特性と関係  (3)

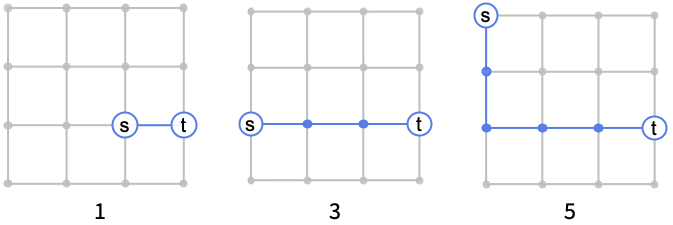
2つの頂点間の距離はFindShortestPathで求めることができる：

距離行列：

連結グラフでは，VertexEccentricityはGraphDistanceで計算できる：

異なる連結成分に属する2つの頂点間の距離はInfinityである：

Wolfram Research (2010), GraphDistance, Wolfram言語関数， https://reference.wolfram.com/language/ref/GraphDistance.html （2015年に更新）.

テキスト

Wolfram Research (2010), GraphDistance, Wolfram言語関数， https://reference.wolfram.com/language/ref/GraphDistance.html （2015年に更新）.

CMS

Wolfram Language. 2010. "GraphDistance." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GraphDistance.html.

APA

Wolfram Language. (2010). GraphDistance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphDistance.html

BibTeX

@misc{reference.wolfram_2024_graphdistance, author="Wolfram Research", title="{GraphDistance}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GraphDistance.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_graphdistance, organization={Wolfram Research}, title={GraphDistance}, year={2015}, url={https://reference.wolfram.com/language/ref/GraphDistance.html}, note=[Accessed: 17-November-2024 ]}