HamiltonianGraphQ

HamiltonianGraphQ[g]

yields True if the graph g is Hamiltonian, and False otherwise.

Details

  • A graph is Hamiltonian if it has a cycle that traverses each vertex exactly once.

Examples

open allclose all

Basic Examples  (2)

Test whether a graph is Hamiltonian:

Not all graphs have a Hamiltonian cycle:

Scope  (6)

HamiltonianGraphQ works with undirected graphs:

Directed graphs:

Multigraphs:

Mixed graphs:

HamiltonianGraphQ gives False for expressions that are not graphs:

HamiltonianGraphQ works with large graphs:

Applications  (2)

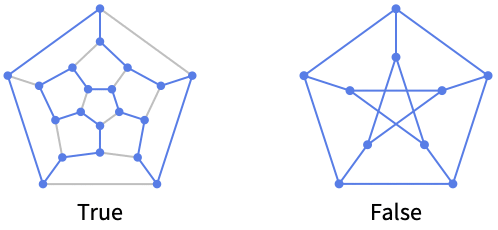
Test whether the Icosian game [MathWorld] has a solution:

A Hamiltonian cycle:

Test whether there is a sequence of moves by a knight chess piece that visits each square of an chessboard exactly once:

Properties & Relations  (4)

A Hamiltonian cycle can be found using FindHamiltonianCycle:

Skeleton graphs of platonic solids are Hamiltonian:

The line graph of a Hamiltonian graph is Hamiltonian:

An Eulerian graph is not always Hamiltonian:

The line graph of an Eulerian graph is Hamiltonian:

Wolfram Research (2010), HamiltonianGraphQ, Wolfram Language function, https://reference.wolfram.com/language/ref/HamiltonianGraphQ.html.

Text

Wolfram Research (2010), HamiltonianGraphQ, Wolfram Language function, https://reference.wolfram.com/language/ref/HamiltonianGraphQ.html.

CMS

Wolfram Language. 2010. "HamiltonianGraphQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HamiltonianGraphQ.html.

APA

Wolfram Language. (2010). HamiltonianGraphQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HamiltonianGraphQ.html

BibTeX

@misc{reference.wolfram_2024_hamiltoniangraphq, author="Wolfram Research", title="{HamiltonianGraphQ}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/HamiltonianGraphQ.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_hamiltoniangraphq, organization={Wolfram Research}, title={HamiltonianGraphQ}, year={2010}, url={https://reference.wolfram.com/language/ref/HamiltonianGraphQ.html}, note=[Accessed: 14-November-2024 ]}