HilbertCurve

HilbertCurve[n]

给出表示第 n^ 步希尔伯特曲线的线段.

HilbertCurve[n,d]

给出 d 维希尔伯特曲线的第 n^ 步.

更多信息和选项

  • HilbertCurve 亦称为希尔伯特空间填充曲线.
  • HilbertCurve[n] 返回一个 Line 基元，对应于从 {0,0}开始，然后连接 2n-1 乘 2n-1 正方形中的所有整数点，在 {2n-1,0} 结束的路径. »
  • HilbertCurve 接受 DataRange 选项，可用来指定坐标应占据的范围.

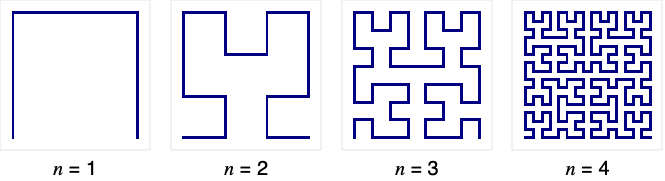
范例

打开所有单元关闭所有单元

基本范例  (2)

二维希尔伯特曲线：

希尔伯特曲线的近似长度：

公式：

用样条线可视化二维希尔伯特曲线：

范围  (8)

曲线指定  (4)

二维希尔伯特曲线：

三维希尔伯特曲线：

维希尔伯特曲线：

近似第 步希尔伯特曲线：

曲线样式  (4)

线段粗细不同的希尔伯特曲线：

线段粗细成比例：

用打印机点指定粗细：

虚线：

颜色不同的曲线：

推广和延伸  (2)

四维希尔伯特曲线：

维希尔伯特曲线：

选项  (1)

DataRange  (1)

DataRange 允许指定所生成的网格坐标的范围：

指定不同的范围：

应用  (4)

可以通过把杯形曲线转换成四个由线段连在一起的杯形曲线来递归式地构建 HilbertCurve：

下一次迭代：

可视化二维希尔伯特曲线：

使用样条线：

三维：

用管子构建：

根据希尔伯特曲线构建多边形：

把希尔伯特曲线样式的纹理放到曲面上：

属性和关系  (3)

HilbertCurve 由线段组成：

计算二维希尔伯特曲线的总长：

三维希尔伯特曲线：

DataRangerange 等价于使用 RescalingTransform[{…},range]：

使用 RescalingTransform：

可能存在的问题  (2)

缺省情况下，希尔伯特曲线的坐标不在单位正方形内：

用 DataRange 来产生位于单位正方形内的希尔伯特曲线：

HilbertCurve 有可能太大，因而无法生成：

巧妙范例  (1)

遍历动画：

Wolfram Research (2017)，HilbertCurve，Wolfram 语言函数，https://reference.wolfram.com/language/ref/HilbertCurve.html.

文本

Wolfram Research (2017)，HilbertCurve，Wolfram 语言函数，https://reference.wolfram.com/language/ref/HilbertCurve.html.

CMS

Wolfram 语言. 2017. "HilbertCurve." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/HilbertCurve.html.

APA

Wolfram 语言. (2017). HilbertCurve. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/HilbertCurve.html 年

BibTeX

@misc{reference.wolfram_2024_hilbertcurve, author="Wolfram Research", title="{HilbertCurve}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/HilbertCurve.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_hilbertcurve, organization={Wolfram Research}, title={HilbertCurve}, year={2017}, url={https://reference.wolfram.com/language/ref/HilbertCurve.html}, note=[Accessed: 21-November-2024 ]}